| 241. | 10 playing cards and a dark room
| | | In a dark room there is a deck of cards with 10 face up and the rest face down. Your task is to divide the total deck into two piles so that the same number of face up cards is in each pile. Remember, it is dark so you can't see the cards. How do you do it?
Answer
Problem 241 Answer
Problem 241 Answer
Place ten cards in one pile with the other 42 cards in the other. Then, flip over the ten-card pile.
Michael Shackleford
Solution
Problem 241 Solution
Problem 241 Solution
Place ten cards in one pile with the other 42 cards in the other. Let's say the 10-card pile has x face up cards and 10-x face down cards. The 42-card pile will have 10-x face up cards.
Then flip over the 10-card pile. It will now have 10-x face up cards, the same as the 42-card pile.
Michael Shackleford
| | | 113. | 10,000 digits of e problem
|   | | The following is a distribution of the first 10,000 digits of e: 0 974
1 989
2 1004
3 1008
4 982
5 992
6 1079
7 1008
8 996
9 968 It is speculated that the number 6 appears a disproportionately high number of times and thus the digits are not distributed randomly. Test the hypothesis that these digits form a random sample such that the outcome of 10,000 truly random digits would pass the test 95% of the time.  Answer
Answer
Problem 113 Answer
Problem 113 Answer
The digits pass the test of randomness.
Michael Shackleford, A.S.A.
Solution
Problem 113 Answer
Problem 113 Solution
Let Q be the chi-squared goodness of fit statistic.
Q = The sum for i=1 to 10 of ( (Ni - npi)2/npi )
= The sum for i=1 to 10 of ( (Ni - 1000)2/1000 )
= (676+121+16+64+324+64+6241+64+16+1024)/1000 = 8.61
According the the chi-squared table with 9 degrees of freedom a Q statistic of greater
than 16.92 shold fail the test. 8.61 is well under 16.92 so it should pass the test. In
other words the digits do appear to be random.
At a level of significance such that 10,000 random digits passed 60% of the time the
10,000 digits of e would still pass, but at a 50% level they would not.
Michael Shackleford, A.S.A.
| | | 190. | 100 coin problem
|   | | There is a table in a dark room with 100 coins. You can't see anything nor feel which sides are up. 80 are heads up and 20 are tails up. Another table in the room has nothing on it. How can you get the same number of coins tails up on both tables with at least one penny on each table?  Answer
Answer
Problem 190 Answer
Problem 190 Answer
First, move any 20 pennies to the other table, keeping the same side on each penny up.
Second, flip all 20 pennies on the other table.
Explanation
Initially table 1 will have 80 heads and 20 tails, and table 2 will have 0 heads and 0 tails.
Let t be the number tails moved, and h be the number of heads.
After the move table 1 will have 80-h heads and 20-t tails, and table 2 will have h heads and t tails.
After the flip table 1 will have 80-h heads and 20-t tails, and table 2 will have t heads and h tails.
So, at this point table 1 has 20-t tails and table 2 has h tails. We moved 20 coins: h heads, and t tails, so h+t=20, or h=20-t. 20-t and h must be the same amount, thus both tables have the same number of tails, although we don't know what that number is.
Thanks to Dan Florentin for this problem.
Michael Shackleford, A.S.A.
| | | 26. | 100 single women problem
|    | | The king has 100 young ladies in his court each with an individual dowry. No two dowrys are the same. The king says you may marry the one with the highest dowry if you correctly choose her. The king says that he will parade the ladies one at a time before you and each will tell you her dowry. Only at the time a particular lady is in front of you may you select her. The question is what is the strategy that maximizes your chances to choose the lady with the largest dowry?
Hint: You should let x ladies go by and choose the first one with a dowry greater than the maximum of the first x. Of course you will pass the highest one if she is among the first x, but that is part of the game.  Answer
Answer
Problem 26 Answer
Problem 26 Answer
You should let 37 ladies go by and select the first
one with a dowry greater than the maximum of the
first 37 dowrys.
Michael Shackleford, A.S.A.
Solution
Problem 26 solution
Problem 26 Solution
Let x be the number of ladies you pass before choosing
the next lady with a dowry greater than the first
x ladies. Let max x be the maximum dowry
in the first x ladies.
The probability of winning is sum for i=x+1 to 100
of the probability that the highest dowry is in the
ith position multiplied by the probability that you
choose it if it is in that position.
This is based on the condition probability formula:
Pr(A)=Sum for i=1 to n of Pr( A | Bi ) * Pr( Bi ),
where the sum for i=1 to n of Pr(Bi)=1.
For all i the probability that the
highest dowry is in that position is 1/100.
The probability that you will choose the dowry if
it is in the ith position is equal to the probability
that the highest of the first i-1 dowries belongs
to one of the first x ladies. This equals x/(i-1). If
the highest dowry of the first i-1 were not in the first x ladies
you would choose it before getting to the largest dowry,
thus losing the game.
For example if you let 30 ladies pass the probability that the
highest dowry is in the 75th postion and that you will choose it
equals 1/100 * 30/74.
Let A denote the overall probability of winning.
The proability of winning given x is the sum for i=x+1 to 100
of x/(i-1) * 1/n. This equals:
Pr(1/n * [ 1 + x/(x+1) + x/(x+2) + ... + x/99 ] ).
Some value of x must be optimal to maximize this formula. This value
of x must the first such that Pr(A|x+1) - Pr(A|x) < 0.
Pr(A|x+1) - Pr(A|x) = 1/n * [ 1/(x+2) + 1/(x+3) + 1/(x+4) + ... + 1/99 - x/(x+1) ].
let y=x+1.
Pr(A|x+1) - Pr(A|x) = 1/n * [ 1/(y+1) + 1/(y+2) + 1/(y+3) + ... + 1/99 - (y-1)/y ]. =
Pr(A|x+1) - Pr(A|x) = 1/n * [ 1/(y+1) + 1/(y+2) + 1/(y+3) + ... + 1/99 - 1 + 1/y ]. =
Pr(A|x+1) - Pr(A|x) = 1/n * [ 1/y + 1/(y+1) + 1/(y+2) + 1/(y+3) + ... + 1/99 - 1 ].
If Pr(A|x+1) - Pr(A|x) = 0, then 1/y + 1/(y+1) + 1/(y+2) + 1/(y+3) + ... + 1/99 = 1.
Theorem: The integral from r to n of 1/x = log(n) - log(r) = log(n/r).
The equation above the theorm is an approximation of the integral in the theorem. By
applying the theorem log(100/y) = 1.
Taking e to the power of both sides: 100/y = e.
y=100/e.
Since e=~2.7182818 y=~36.79, since x=y-1 x=~35.79.
Since the integral is an underestimate of the series look at some specific
values of Pr(A) for values of x close to 35.79:
x A
--- ---
35 37.0709%
36 37.1015%
37 37.1043%
38 37.0801%
So the optimal strategy is to let 37 ladies pass and then
choose the first lady with a dowry larger than the greatest of the first 37.
In general the answer is going to be n/e, where n is the total
number of ladies. Because the answer must be an
exact integer and error in applying the theorem mentioned above you should
check the few integers just above the optimal value. As n increases the
error decreases. The probability of winning turns out to approach 1/e =~ 36.79%
as n approaches infinity (I'll leave this proof up to you).
Here are some optimal values of x for various values of n and
the probability of winning given x:
n x Pr(winning)
---- --- -----------
3 2 50.00%
4 2 43.83%
5 3 43.33%
6 3 42.78%
7 3 41.43%
8 4 40.98%
9 4 40.60%
10 4 39.87%
15 6 38.94%
20 8 38.42%
30 12 37.87%
50 19 37.42%
100 38 37.10%
1000 369 36.82%
For more information I suggest section 2.5 of Probability and Statistics,
second edition by Morris H. DeGroot.
Here another version of my solution to this problem
Let x be the number of ladies you pass before choosing
the next lady with a dowry greater than the first
x ladies. Let maxx be the maximum dowry
in the first x ladies.
The probability you will select the highest dowry is:
Sum for i=1 to 100-x of: ( Probability that i of the
remaining ladies will have a dowry greater than maxx )
* (1/i).
This probability for any i is:
(100-x)*(99-x)*(98-x)*...*(101-x-i) * x
---------------------------------------
100*99*98*...*(100-i)
For example suppose you let 30 ladies go my first and planned to
choose the next one with a dowry greater than the maximum of
the first 30. max 30 is the largest dowry of the
first 30 ladies. Let Pr(n i) equal the probability
that there are i ladies left with a dowry greater than max x.
The probability of you winning would be:
Pr(n1) * 1 +
Pr(n2) * 1/2 +
Pr(n3) * 1/3 +
Pr(n4) * 1/4 +
Pr(n5) * 1/5 +
.
.
.
Pr(n70) * 1/70.
To derive Pr(ni) consider the probability that the i highest
dowrys fall in the last 100-x ladies, multiplied the the probability that
the (i+1)th highest dowry falls in the first x ladies. For example:
Pr(n3) = 70/100 * 69/99 * 68/98 * 30/97.
70/100 = Probability that the highest dowry is not in first 30.
69/99 = Probability that the second highest dowry is not in first 30 (99 positions left, 69
not if first 30).
68/98 = Probability that the third highest dowry is not in first 30.
30/97 = Probability that fourth highest dowry is in first 30.
Personally I had to use a spreadsheet to find that the maximum
probability was for x=37, which was 37.1%.
If you change the number of total ladies from 100 to any other number the strategy
seems to still be to let 37% of them go by first.
Michael Shackleford, A.S.A.
| | | 127. | 100 story building and a billiard ball problem
|   | | It is your task to determine how high you can drop a billiard ball without it breaking. There is a 100 story building and you must determine which is the highest floor you can drop a ball from without it breaking. You have only two billiard balls to use as test objects, if both of them break before you determine the answer then you have failed at your task. How can you determine the breaking point in which the maximum necessary dropping is at a minimum. Click on 'answer' for just the minimum maximum and 'solution' for how to determine the breaking point under this minimum.  Answer
Answer
Problem 127 Answer
The minimum maximum number of droppings is 14.
Michael Shackleford, A.S.A., 10/31/1998
Solution
Problem 127 Solution
First drop the first ball from the 14th floor. If it breaks you can
determine the exact breaking point with the other ball in at most
13 more droppings, starting at the bottom and going up one floor
at a time.
If the first ball survives the 14 floor drop then drop it again
from the 27th (14+13) floor. If it breaks you can determine the exact
breaking point with at most 12 more droppings.
If the first ball survives the 27 floor drop then drop it again
from the 39th (14+13+12) floor. If it breaks you can determine the exact
breaking point with at most 11 more droppings.
Keep repeating this process always going up one less floor than the
last dropping until the first ball breaks. If it breaks on the xth dropping you will only need at most 14-x more droppings
with the second ball to find the breaking point. By the 11th dropping
of the first ball, if you get that far, you will have reached the
99th floor.
Thanks to Alon Amit for this problem.
Michael Shackleford, A.S.A., 10/31/1998
| | | 84. | 12 pearls and a scale problem
|    | | In front of you are 12 pearls, 11 being real and one fake. The real ones all weigh the same and the fake one differs in weight from the real ones (may weigh more or less). With a balance scale and three weighings how can you weed out the fake one and determine whether it is too heavy or too light?  Answer
Answer
Problem 84 Answer
Problem 84 Answer
Note: The following solution may not be the only one possible. At least one other solution has been submitted to me.
First weigh any 4 pearls against any other 4.
If one side weighs heavier than the other then:
Label the pearls on the heavy side H, the pearls on the light side L, and the
4 other pearls G. Next, weigh two H pearls and two L pearls against 2 G pearls, 1 H pearl, and 1 L pearl
(HHLL vs GGHL).
If the HHLL side goes down then either one of the two H pearls on the left
side from step 2 is heavy or the L pearl on the right side of step 2 is light. Finally
weigh ( HL vs GG ). If the HL side goes down the H pearl is heavy, if the HL side goes up
the L pearl is light, if they stay the same the other H pearl is heavy.
If the HHLL side (from step 2) goes up then either one of the two L pearls on the left
side from step 2 is light or the H pearl on the right side of step 2 is heavy. Finally
weigh ( HL vs GG ). If the HL side goes down the H pearl is heavy, if the HL side goes up
the L pearl is light, if they stay the same the other L pearl is light.
If the two sides from step 2 stay the same you have left one H pearl and one L pearl.
Weigh ( HL vs GG ). If the left side goes down the H pearl is heavy, if it goes up the
L pearl is light.
If the two sides from step one stay the same then label the 8 pearls used in step 1 as
G and the 4 others pearls as B. For the second weighing weigh 3 B pearls against
3 G pearls ( BBB vs GGG).
If the left side goes down one of the B pearls is heavy. Weigh them 2 of
them against each other
the heavy side will have the heavy pearl, if the sides stay the same the
other pearl is heavy.
If the left side goes up one of the B pearls is light. Weigh them 2 of
them against each other
the light side will have the light pearl, if the sides stay the same the
other pearl is light.
If the two sides from the second weighing stay the same then the last B
pearl is heavy or light. Use the third weighing against a good pearl
to determine if it is heavy or light.
Michael Shackleford, A.S.A.
| | | 80. | 128 pennies and a blindfold problem
|   | | You are blindfolded before a table. On the table are a very large number of pennies. You are told 128 of the pennies are heads up and the rest are tails up. How can you create two subgroups of pennies, each with the same number of heads facing up?  Answer
Answer
Problem 80 Answer
Problem 80 Answer
Create a subgroup of any 128 pennies. Then flip over all 128. That group of
128 and the group of all the remaining pennies will have the same number of heads
facing up.
Michael Shackleford, A.S.A., February 4, 1999
| | | 118. | 13 pirates and a safe problem
|   | | Thirteen pirates put their treasure in a safe. They decide that the safe should be able to be opened if any majority of pirates agree but not be able to be opened if any minority agree. The pirates don't trust each other so they consult a locksmith. The locksmith puts a specific number of locks on the safe such that every lock must be opened to open the safe. Then he distributes keys to the pirates such that every pirate has some but not all of the keys. Any given lock can have multiple keys but any given key can only open one lock. What is the least number of locks required?  Answer
Answer
Problem 118 Answer
Problem 118 Answer
1716 locks are required.
Michael Shackleford, A.S.A.
Solution
Problem 118 Solution
Problem 118 Solution
The number of ways you can choose 7 out of 13 pirates is 13!/(7!*6!) = 1716, where x! = 1*2*...*x.
Next put 1716 locks on the safe, one for each way to group 7 pirates. For each lock give 7 keys to
a unique group of 7 pirates. This way any given lock
will have a keyholder in any group of 7 or more. For any group of 6 there will be exactly one lock
in which the other 7 pirates have the key. Obviously any group of less than 6 would also be missing
at least one key to at least one lock.
Here are the number of keys required for other numbers of pirates:
Number
of
Pirates Number of Locks
------- -------------------
3 3
5 10
7 35
9 126
11 462
13 1,716
15 6,435
17 24,310
19 92,378
21 352,716
23 1,352,078
25 5,200,300
27 20,058,300
29 77,558,760
31 300,540,195
33 1,166,803,110
35 4,537,567,650
37 17,672,631,900
39 68,923,264,410
41 269,128,937,220
43 1,052,049,481,860
45 4,116,715,363,800
47 16,123,801,841,550
49 63,205,303,218,876
51 247,959,266,474,050
53 973,469,712,824,060
Michael Shackleford, A.S.A.
| | | 204. | 154 Rolls of the Dice in Craps
|    | | On May 23, 2009, a craps player held the dice for 154 rolls at the Borgata casino in Atlantic City (source). What is the probability of going 154 rolls or longer in craps? Please give an expression of the answer and/or a numeric answer.  Answer
Answer
Problem 204 Answer
Problem 204 Answer
Question
On May 23, 2009, a craps player held the dice for 154 rolls at the Borgata casino in Atlantic City (source). What is the probability of going 154 rolls or longer in craps? Please give an expression of the answer and/or a numeric answer.
Answer
The answer is P1 + P2 + P3 + P4, where
[ P1 ] [12 3 4 5]^153 [1]
[ P2 ] [ 6 27 0 0] [0]
[ P3 ] = (1/36)^153 × [ 8 0 26 0] × [0]
[ P4 ] [10 0 0 25] [0]
The exact answer is:
P1 = 3.12763 × 10-11
P2 = 4.63460 × 10-11
P3 = 4.95558 × 10-11
P4 = 5.17044 × 10-11
The sum of these probabilities is 1.78882 × 10-10 = 1 in 5,590,264,072
Acknowledgement: My thanks to BruceZ for this help with this problem.
Michael Shackleford, ASA — June 2, 2009
Solution
Problem 204 Solution
Problem 204 Solution
Question
On May 23, 2009, a craps player held the dice for 154 rolls at the Borgata casino in Atlantic City (source). What is the probability of going 154 rolls or longer in craps? Please give an expression of the answer and/or a numeric answer.
Answer
Solution
There are four possible states the shooter can be in. Let's define them as follows.
State 1 = Come out roll
State 2 = Point of 4 or 10
State 3 = Point of 5 or 9
State 4 = Point of 6 or 8
The probabilities are recursive. Let p(x,r) represent the probability of being in state x before roll r. Based on simple dice probabilities, p(x,r) can be expressed as follows:
(1) P(1,r) = (12/36)×p(1,r-1) + (3/36)×p(2,r-1) + (4/36)×p(3,r-1) + (5/36)× p(4,r-1)
(2) P(2,r) = (6/36)×p(1,r-1) + (27/36)×p(2,r-1)
(3) P(3,r) = (8/36)×p(1,r-1) + (26/36)×p(3,r-1)
(4) P(4,r) = (10/36)×p(1,r-1) + (25/36)×p(4,r-1)
In more plain simple English, equation (1) is saying that the probability of being in a come out roll before roll r is the sum of the following:
- Product of the probability of being in a come out roll the previous turn, and the probability of staying in a come out roll (12/36).
- Product of the probability of rolling for a 4 or 10 the previous roll, and the probability of making the point (3/36), resulting in a come out roll.
- Product of the probability of rolling for a 5 or 9 the previous roll, and the probability of making the point (4/36), resulting in a come out roll.
- Product of the probability of rolling for a 6 or 8 the previous roll, and the probability of making the point (5/36), resulting in a come out roll.
Equation (2) is saying the probability of rolling for a 4 or 10 before roll r is the sum of:
- Product of the probability of being in a come out roll the previous turn, and the probability of rolling a 4 or 10 (6/36).
- Product of the probability of rolling for a point of 4 or 10 the previous turn, and the probability of not rolling the desired point or a 7 (27/36).
Equation (3) is saying the probability of rolling for a 5 or 9 before roll r is the sum of:
- Product of the probability of being in a come out roll the previous turn, and the probability of rolling a 5 or 9 (8/36).
- Product of the probability of rolling for a point of 5 or 9 the previous turn, and the probability of not rolling the desired point or a 7 (26/36).
Equation (4) is saying the probability of rolling for a 6 or 8 before roll r is the sum of:
- Product of the probability of being in a come out roll the previous turn, and the probability of rolling a 6 or 8 (10/36).
- Product of the probability of rolling for a point of 6 or 8 the previous turn, and the probability of not rolling the desired point or a 7 (25/36).
Next, let's express the these four equations in the form of a matrix.
[ P(1,r) ] [12 3 4 5] [ P(1,r-1) ]
[ P(2,r) ] [ 6 27 0 0] [ P(2,r-1) ]
[ P(3,r) ] = (1/36) × [ 8 0 26 0] × [ P(3,r-1) ]
[ P(4,r) ] [10 0 0 25] [ P(4,r-1) ]
The intial roll is always a come out roll, so the initial state is:
[ 1 ]
[ 0 ]
[ 0 ]
[ 0 ]
The probability of each state before the 154th roll is expressed as follows. The reason we take the matrix to the 153rd power, and not the 154th, is there are 153 transformations since the initial state.
[ P(1,154) ] [12 3 4 5]^153 [1]
[ P(2,154) ] [ 6 27 0 0] [0]
[ P(3,154) ] = (1/36)^153 × [ 8 0 26 0] × [0]
[ P(4,154) ] [10 0 0 25] [0]
The exact answer is:
P(1,154) = 3.12763 × 10-11
P(2,154) = 4.63460 × 10-11
P(3,154) = 4.95558 × 10-11
P(4,154) = 5.17044 × 10-11
The sum of these probabilities is 1.78882 × 10-10 = 1 in 5,590,264,072
Acknowledgement: My thanks to BruceZ for this help with this problem.
Michael Shackleford, ASA — June 2, 2009
| | | 132. | 21 squares in a big square problem
|     | | Find a way to fit 21 squares, each with a unique integer side length, that can be arranged into the shape of a square (this problem is very challenging).
Answer
Problem 132 Answer
Problem 132 Answer

The following are the lengths of the various sides, according to
the lables in the image:
a=50
b=35
c=27
d=8
e=19
f=15
g=17
h=11
i=6
j=24
k=29
l=25
m=9
n=2
o=7
p=18
q=16
r=42
s=4
t=37
u=33
Thanks to Terry W. Ryder of San Leandro, CA and
New Scientist magazine for the problem and Terry for the graphic.
This problem inspired my friend Dick Tucker to not only solve the
problem but create a piece of art with it using acrylic plexiglas.
 Michael Shackleford, A.S.A., February 23, 1999
Michael Shackleford, A.S.A., February 23, 1999
Solution
Problem 132 Solution
Problem 132 Solution

Cosinder all the ways you can define the length of an edge of the outer
square, where each variable represents the length of the side or the
corresponding square in the image:
- a+b+c
- a+b+d+e
- a+f+g+h+e
- a+f+g+i+j
- k+l+m+n+g+h+e
- k+l+m+n+g+i+j
- k+l+m+o+p+j
- k+l+q+p+j
- k+l+q+r
- k+s+t+r
- u+t+v
- a+k+u
- a+l+s+u
- a+l+t
- b+f+l+s+u
- b+f+l+t
- b+f+m+q+t
- b+f+n+o+q+t
- b+g+o+q+t
- b+g+q+r
- b+h+i+p+r
- b+h+j+r
- c+d+h+i+p+r
- c+d+h+j+r
- c+e+j+r
Next take 21 of these equations and set them equal to 1. You can not
just use any 21, I would suggest taking out four from various places among
the list as opposed to four in a row. After taking out four of the above equations
I was left with the following matrix:
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
Then use Cramer's Rule to solve the equations. In Excel the MDETERM(a1:u21)
command will give you the determinant of the matrix bounded by a1 and u21,
making this process quick and mostly automated. If the determinant used for
the denominator is zero then choose a different set of 21 equations.
When solving for a..u ignore the deonominator determinant since it will
be the same for all 21 variables. After solving for all 21 looking for
common factors among the solutions and divide.
Thanks to Terry W. Ryder of San Leandro, CA and
New Scientist magazine for the problem and Terry for the graphic.
Michael Shackleford, A.S.A., February 23, 1999
| | | 219. | 23 prisoners and two light switches problem
| | | There is a prison with 23 prisoners. The warden brings all the prisoners to a meeting and explains that he set up a room with two switches, labeled A and B. Each can be in an on or off position only. Starting the next day, the warden will pick a prisoner at random, with replacement, once per day. That prisoner will be led to the switches room. He must then switch one, and only one, switch of his choice.
When any member of the group declares "We have all been to the switch room," the warden will check his records to see if it is true. If it is true, then each prisoner will be set free immediately. If not, they will all be given the death penalty immediately.
The warden explains they can have the rest of the day to discuss strategy. Then they will all be separated and will never have a chance to communicate again, except via how they set the switches.
One final detail, the warden will set the switches in their initial state at random and not inform the prisoners beforehand of the initial setting.
Answer Problem 219 Answer
There are various solutions to the problem but most are variants of the one below. I believe my answer will get the prisoners released in the least number of expected days.
- The prisoner called to the switch room on the first day will be designated the leader. If switch A is in the up position, then he will flip in the down position. If it is already down, he will flip switch 2 (the dummy switch). He will start his running count of visits to 1.
- Starting with the second day, do the following:
- If a non-leader is called, and switch A is down position, and he has never fipped switch A, then he will flip switch A to the up position. This is the way to announce that one more person has visited the switch room.
- Otherwise, if a non-leader is called into the switch room, and any of the conditions are not met, then he should flip switch B.
- If the leader is called back into the room and switch A is in the up position it means a new prisoner has entered. The leader will flip A down and add one to his running count.
- If the leader is called back into the room and switch A is in the down position then it will mean no new prisoner has entered the room since the last time he was there. He will flip switch B.
- When the leader reaches a running count of 23, he can safely declare that everyone has been to the switch room at least once.
This method requires an average of 22*23 + sum for i=1 to 22 of 23/(23-i), which equals 591.8887 days.
Michael Shackleford, March 25, 2017
| | | 221. | 25 horses problem
| | | You have 25 horses and a track that can race five horses at a time. The only thing you learn from each race is the winning order, from 1 to 5. You don't have a watch. Each horse always runs at its own constant speed. What is the least number of races required to determine the fastest three horses in order and how should it be done?
Answer Problem 221 Answer
The answer is 7.
Michael Shackleford, June 11, 2017
Problem 221 Solution
- Divide the 25 horses into five groups of five.
- Races 1-5: Race each group and note the top three horses, in order. Call these the heats.
- Race 6: Race the winner of each race from step 2. The winner of this race will be the fastest horse.
- Race 7: Race the the following five horses:
- Second and third place horses from race 6.
- The two horses from the group of five second place horses from step 1 that finished second in its heat to the winning two horses in race 6.
- The horse from the third place group that finished third in its heat to the winning horse in race 6.
There is a good explanation at A Collection of Quant Riddles With Answers of why this solution works.
Michael Shackleford, ASA — April 5, 2017
| | | 239. | 3 hot dog vendors and a beach
| | | There is a beach one mile long. It is a nice day so a big crowd of people are expected, who will be equally distributed along the beach. When anyone gets hungry, he heads to the nearest hot dog stand. Three logicians operate hot dog carts and arrive to the beach one at a time before the crowds arrive. A is first, then B, and finally C. All three will locate their stand with the goal of maximizing sales for the day. Once a spot is picked, the vendor must stay there all day. The vendors don't trust each other, so collusion is out. B will note the location of A and choose his location accordingly. C will note the locations of A and B and pick his location accordingly. Where should A set up his stand? How much of the beach will each vendor get, assuming all follow optimal strategy. You may assume that if a vendor is indifferent between multiple locations, then he will pick randomly.
Answer
Problem 239 Answer
Problem 239 Answer
The first should go either a smidge to the left of the point 1/4 from the left end of the beach and a smidge to the right of the point 3/4 from the right end.
The second vendor will pick the spot from A's two choices that A didn't pick.
The third vendor will go in the middle.
This will give A and B 3/8 of the beach each, and C 1/4.
Michael Shackleford
Solution
Problem 239 Solution
Problem 239 Solution
It stands to reason that A and B will want C to go in the middle, least he be the closest to an edge and cut them off from that section of the beach. How far can they extend away from an edge and still keep C in the middle?
Let's call x the distance from either edge that would put C indifferent between going right next to A and B but closer to an edge and the middle.
At x, assuming C goes in the middle, A will get x + (0.5 - x)/2 = x/2 + 1/4 of the beach. Same with B. C will bet (1-2x)/2 = 1/2 - x of the beach.
If C located right next to A or B, but closer to an edge, he would get territory of length x. So, we want to equate x and (1/2 - x) to find that indifference point for C.
x = 1/2 - x
2x = 1/2
x = 1/4
To make sure C isn't indifferent, and barely prefers the middle, A and B should go just a smidge closer to the edges than the 1/4 and 3/4 points. This will give A and B a smidge less then 3/8 of the beach each and C a smidge more than 1/4.
Michael Shackleford
| | | 240. | 4 hot dog vendors and a beach
| | | Same problem as 239, except four vendors.
Answer
Problem 240 Answer
Problem 240 Answer
A will set is stand a smidge less than 1/6 of a mile from either end.
B will do the same as A, but at the opposite end.
C will set his stand exactly in the middle of the beach.
D will be indifferent between placing his stand between either (1) A and C and (2) B and C.
Michael Shackleford
Solution
Problem 240 Solution
Problem 240 Solution
A will want to pick a spot close to either edge, maximizing his space without giving another vendor the incentive to put his stand right next to his on the side close to the edge. It is good to be close to an edge, because you get every customer between you and that edge. Let's just say he picks the left side of the beach.
B will want to do the same, but on the right side.
C will pick a spot in the middle, putting D to an indifference point which side of C to go on.
D will arbitrarily pick a spot between A and C or B and C.
The question is how far from the edge should A and B pick?
We want D to pick on either side of C. Let's ask the question at what point would D be indifferent between going just to the left of A, between A and C, and between B and C.
If A sets his stand at point x, then D would get x miles just to the left of A or (1/2-x)/2 by going between A and C or B and C. Let's set these two equations equal to each other and solve, to find the indifference point for x.
x = (0.5-x)/2
2x = 0.5 - x
3x = 0.5
x = 1/6
However, we don't want D to be indifferent, we want him to pick a spot on either side of C. So, we pick a spot a smidge to the left of 1/6, to get D to go next to C.
Same logic for B -- a smidge to the right of 5/6.
C will want to make D indifferent to going on either side of him, which is obviously 1/2.
D will then arbitrarily picks between 1/3 and 2/3.
A will then get 1/4 if D picks 3/8 and 1/3 if he picks 5/8. The average of those two is 7/24.
B is in the same situation as A, so 7/24 on average to him too.
Let's say D flips a coin and goes in the 1/3 spot. Then C will get everything from the 5/12 to the 2/3 point, which is 1/4 mile.
With D and the 1/3 spot, he will everything from the 1/4 to the 5/12 points, which is 1/6 mile.
Michael Shackleford
| | | 165. | 64-minute fuse problem
|   | | You have a box of matches and six 64-minute fuses. Each fuse burns exactly 64 minutes but the rate of burning is inconsistent. A half a fuse would not necessarily burn in 32 minutes. The fuses are also not equally inconsistent. Two cut fuses of the same length would not necessarily burn in the same time. Without the use of a clock, scissors, or anything other than the matches and the fuses how can you create a 60-minute fuse?  Answer
Answer
Problem 165 Answer
Problem 165 Answers
Following is my original solution.
- At time t=0 light fuse 1 at both ends and fuses 2, 3, 4, and 5 at one end. Fuse 1 will have 32 minutes remaining, fuses 2-5 will have 64 minutes remaining.
- At time t=32 fuse 1 will have burned out. At this moment light fuse 2 at the other end. Fuse 2 will have 16 minutes remaining, fuses 3-5 will have 32 minutes remaining.
- At time t=48 fuse 2 will have burned out. At this moment light fuse 3 at the other end. Fuse 3 will have 8 minutes remaining, fuses 4,5 will have 16 minutes remaining.
- At time t=56 fuse 3 will have burned out. At this moment light fuse 4 at the other end. Fuse 4 will have 4 minutes remaining, fuse 5 will have 8 minutes remaining.
- At time t=60 fuse 4 will have burned out. At this moment start fuse 6. Fuse 5 will have 4 minutes remaining, fuse 6 will have 64 minutes remaining.
- At time t=64 fuse 5 will have burned out. At this moment snuff out fuse 6. Fuse 6 will have 60 minutes remaining when relit.
Next is another solution submitted by Michael Nolan.
Solution 2
- At time t=0 light fuse 1 at both ends and fuse 2 at one end. Fuse 1 will have 32 minutes remaining and fuse 2 will have 64 minutes remaining.
- At time t=32 fuse 1 will have burned out. At this moment light the other end of fuse 2 and fuse 3 at one end. Fuse 2 will have 16 minutes remaining and fuse 3 will have 64 minutes remaining.
- At time t=48 fuse 2 will have burned out. At this moment light fuse 3 at the other end and light fuse 4 at one end. Fuse 3 will have 24 minutes remaining and fuse 4 will have 64 minutes remaining.
- At time t=72 fuse 3 will have burned out. At this moment light fuse 5 from both ends. Fuse 4 will have 40 minutes remaining and fuse 5 will have 32 minutes remaining.
- At time t=104 fuse 5 will have burned out. At this moment light fuse 4 from the other end and light fuse 6 from one end. Fuse 4 will have 4 minutes remaining and fuse 6 will have 64 minutes remaining.
- At time t=108 fuse 4 will have burned out. At this moment snuff out fuse 6. Fuse 6 will have 60 minutes remaining.
Next is another solution submitted by Michael Nolan and Andy 'Deuce' Smith.
Solution 3
- Light #1 at both ends, and #2 and #3 at one end. Unlight #2 and #3 when #1 burns out. This makes #2 and #3 both 32-minute fuses.
- Light #2 at both ends, and #4 at one end. Unlight #4 when #2 burns out. This makes #4 a 48-minute fuse.
- Light #4 at both ends, and #3 at one end. Unlight #3 when #4 burns out. This makes #3 an 8-minute fuse.
- Light #3 at both ends, and #5 at one end. Unlight #5 when #3 burns out. This makes #5 a 60-minute fuse.
Next is another solution submitted by Michael Nolan and Kenneth R. Smith.
Solution 4
- At time t=0 light fuse 1 at both ends and fuses 2, 3, and 4 at both ends. Fuse 1 will have 32 minutes remaining, fuses 2-4 will have 64 minutes remaining.
- At time t=32 fuse 1 will have burned out. At this moment light fuse 2 at the other end. Fuse 2 will have 16 minutes remaining, fuses 3,4 will have 32 minutes remaining.
- At time t=48 fuse 2 will have burned out. At this moment light fuse 3 at the other end. Fuse 3 will have 8 minutes remaining, fuses 4 will have 16 minutes remaining.
- At time t=56 fuse 3 will have burned out. At this moment light fuse 4 at the other end and fuse 5 at one end. Fuse 4 will have 4 minutes remaining and fuse 5 will have 64 minutes remaining.
- At time t=60 fuse 4 will have burned out. At this moment snuff out fuse 5. Fuse 5 will have 60 minutes remaining when relit.
Credit and thanks for this problem goes to Craig Olson, Alan Goldberg, and the Nov/Dec 1999 Contingencies magazine.
Michael Shackleford, ASA - July 1, 2001
| | | 97. | A dog, a chain, and a lighthouse problem
|     | | A dog is chained to a point of the side of a circular lighthouse of radius 1. The length of the dog's chain is pi. The dog may not go inside the lighthouse. How much area can the dog cover?  Answer
Answer
Problem 97 Answer
Problem 97 Answer
The answer is 5/6 *pi 3.
Michael Shackleford, A.S.A.
Solution
Problem 97 Solution
Problem 97 Solution
Lets call x the angle formed by (1,0), (0,0), and the point where dog's chain
leaves the edge of the lighthouse, assuming the dog is trying it extending as
far as possible causing the straight part of the chain to be tanjent to the
edge of the lighthouse. For now lets only concern ourselves with the area
to the right of x=-1 and above y=0.
Since the radius of the lighthouse is 1 the length of the straight part of the
chain is the same as x. Through a little trigonomtry we can get the coordinates
of the dog given x as (cos(x)+x*sin(x),sin(x)-x*cos(x)). The distance from
(0,0) to the dog, given x, conveniently works out to (1+x2)1/2,
using the length of a line segment formula.
Lets call y the angle fromed by (1,0), (0,0), and the location of the dog.
Through some more trigonomty (again left up to you) we can solve for y
in terms of x as y=x-tan-1. Now we are ready to integrate.
The area in terms of polar coordinates is 1/2 * the integral over the range
of the angle of the radius squared. We can not simply take the integral from
0 to Π of 1+x2 because this is not the radius formed by the angle
x, but the radius formed by y. We could take the integral over the range of
the angle y but finding the coordinates of the dog in terms of y is very hard
(I couldn't do it). However we can take the ingregal as x goes from 0 to
Π of 1+x2 multiplied by the change in y given a change a change
in x. Since y=x-tan-1(x). dy/dx = 1-1/(1+x2)!
So now the area becomes the integral as x goes from 0 to Π of 1/2 the product
of 1+x2 and 1-1/(1+x2) which equals 1/2 the integral from
0 to Π of x2 which equals Π3/6.
This integral, however, does not cover the area bounded by the triangle (0,0), (-1,0) and
(-1,Π). So we must add this area which is Π/2. Yet we must subtract the area
inside the lighthouse which the dog may not go in, which is also Π/2. So these
two modifications conventiently cancel each other out.
The area of the quarter circle to the left of x=-1 and above y=0 is Π3/4,
since the length of the chain is Π and the dog covers a semicircle to the left of the
lighthouse. So the total area above y=0 is 5/12 * Π3. Finally double
this for the area under y=0 and the total area is 5/6 * Π3
Here is another solution I received from Patrick.

I would like to thank Steven Lutz for sending me
this problem.
Michael Shackleford, A.S.A.
| | | 32. | A fence, board, and a shadow problem
|   | | You have a 6 foot fence and at 15 foot board. The sun is shining directly overhead. You want to lean your board against the fence so that as large a shadow as possible covers your neighbor's yard. What is the maximum length of the shadow you can form? The ladder must rest against the fence and touch the ground on your side of the fence.  Answer
Answer
Problem 32 Answer
Problem 32 Answer
The answer is (540 2/3-36) 1/2 * (15/540 1/3-1) =~ 4.635873 feet.
The shadow over your yard is (5402/3-36)1/2 =~ 5.505698 feet.
The angle formed is approximately 47.46 degrees.
Michael Shackleford, A.S.A.
Solution
Problem 32 Solution
Problem 32 Solution
Let x be the shadow over your yard.
Let y be the shadow over neighbor's yard.
By similar triangles: x/(36+x2)1/2=(x+y)/15.
y=15x/(36+x2)1/2-x.
y'=(((15*(36+x2)1/2)-(15x2*(36+x2)-1/2))
/ 36+x2) - 1.
Then set y'=0 and solve for x.
Finally subsitute x in the similar triangles formula to solve for y.
Michael Shackleford, A.S.A.
| | | 72. | A jar and an amoeba problem
|   | | A jar begins with one amoeba. Every minute, every amoeba turns into 0, 1, 2, or 3 amoebae with probability 25% for each case ( dies, does nothing, splits into 2, or splits into 3). What is the probability that the amoeba population eventually dies out?  Answer
Answer
Problem 72 Answer
The answer is sqr(2)-1 =~ .414213562
Michael Shackleford, A.S.A.
Solution
Problem 72 Solution
Let p be the probability that just one amoba eventually dies out, and all its
decendants. The probablity of n amoba all dying out is pn.
After the first turn there are four possibilities for the number of
amoba left, 0, 1, 2, 3 with probabilites of eventually dying out of
0, p, p2, and p3. With each outcome being
equally likely the probability of all amoba eventually dying out is
1/4*[ 1 + p + p2 +
p3 ]. So p = 1/4*[ 1 + p + p2 + p3 ] or
1 -3p + p2 + p3 = 0. This reduces to
(p - 1)(p2 + 2p - 1) = 0.
The solutions for p are 1, (sqr(2)-1), and (-sqr(2)-1). The only one
which satisfies the constraints of the problem is sqr(2)-1.
Michael Shackleford, A.S.A.
| | | 150. | ABCDE * 4 = EDCBA problem
|  | | ABCDE * 4 = EDCBA. Solve for A,B,C,D, and E where each is a unique integer from 0 to 9.  Answer
Answer
Problem 150 Answer
Problem 150 Answer
ABCDE=21978.
Michael Shackleford, ASA, December 28, 1999
Solution
Problem 150 Solution
Problem 150 Solution
It is obvious that A can be no more than 2. If A were 3 then 3BCDE * 4 would be
at least 120,000 which is more than five digits. Also A must be an even number
because EDCBA is an even number since it is the product of at least one even
number (4). We can eliminate A=0 because E would have to be 5 (5*4=0) but BCDE*4
could not hope to reach 50,000. So A must be 2.
Next consider E. E*4 must end in the digit 2. The only numbers that works for are
3 and 8. However with A=2 EDCBA must be at least 80,000. So 8 is the only number
that satisifies both conditions.
Next consider B. We already know that 2BCD8*4 is at least 80000 and less than
90000. B can not be more than 2 because then 2BCD8 * 4 would be more than
80000. 2 is already taken so B must be 0 or 1. Lets consider the case that
B=0. Then D8 * 4 must end in the digit 02. However there is no D that satisfies
this condition. So B must be 1.
Next consider D. D8*4 must end in the digits 12. The only possiblity is D=7
(78*4=312).
Now solve for C:
21C78 * 4 = 87C12.
84312+400C = 87012 + 100C
2700 = 300C
C=2700/300=9.
So ABCDE=21978.
I'd like to thank "Marisa" for this problem.
Michael Shackleford, ASA, December 28, 1999
| | | 179. | Acceleration problem
|   | | A drag racer accelerates at a uniform rate from its starting point. It travels the last one fourth of the distance from the starting point to the finish line in 3 seconds. How long did it take to travel the entire distance from starting point to finish line?  Answer
Answer
Problem 179 Answer
Problem 179 Answer
The answer is 12 + 6*3 1/2 =~ 22.39230485
Michael Shackleford, ASA - December 14, 2000
Solution
Problem 179 Solution
Problem 179 Solution
Let the total distance traveled be 1.
Let a be the acceleration.
Let t be the total time traveled.
Basic calculus tells us that the velocity at time t is a*t and the total distance traveled is a*t2/2.
So we know:
(1) 1=a*t2/2 and
(2) 0.75 = a*(t-3)2/2
Solving both sides for a we have :
(3) 2/t2 = 3/(2*(t-3)2)
4*(t-3)2 = 3*t2
t2 - 24t + 36 = 0
t = (24 +/- 4321/2)/2
(11) t = 6*31/2 + 12
Add 3 for the total distance of 12 + 6*31/2 =~ 22.39230485
Michael Shackleford, ASA - December 6, 2000
| | | 27. | Alley and two ladders problem
|   | | There is a 6 foot wide alley. Both walls of the alley are perpendicular to the ground. Two ladders, one 10 feet long, the other 12 feet, are propped up from opposite corners to the adjacent wall, forming an X shape. All four feet of each ladder are firmly touching either the corner or the wall. The two ladders are also touching each other at the intersection of the X shape. What is the distance from the point of intersection to the ground? 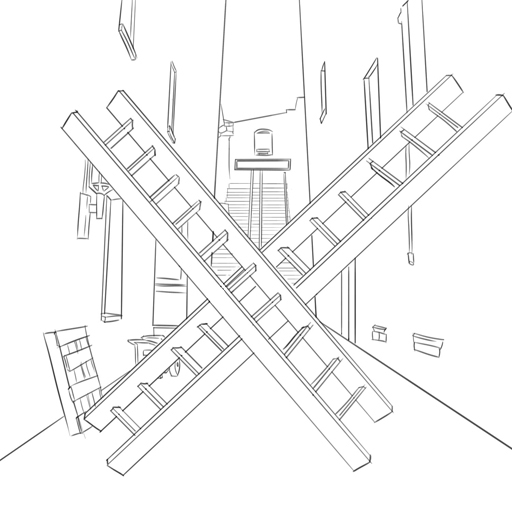 Answer
Answer
Problem 27 Answer
Problem 27 Answer
The answer is 108 1/2/(1+(108 1/2/8)) =~ 4.52 feet.
Michael Shackleford, A.S.A.
Solution
Problem 27 solution
Problem 27 Solution
Solution 1
Consider the two ladders two lines on a graph. Let the shorter ladder extend from
(0,0) to (6,8). Let the longer ladder extend from (6,0) to (0,1081/2).
The square root of 108 can be found using the pythagorean formula.
Then solve for the slope and y intercept to find the equations of the two lines:
The shorter ladder have the equation y=(4/3)*x.
The longer ladder has the equation y=(-1081/2/6)*x + 1081/2.
The lines meet where the ladders cross.
Use substitution to solve for y.
Acknowledgement: Thanks to Steve Lutz for suggesting this
method of solution.
Solution 2
Scott R. Walshon pointed out that if x and y are the heights where the ladders touch the wall, and p is the height of the intersection then 1/p = 1/x + 1/y.
To prove this let x be the height on the right wall and y the height on the left wall. Call a the distance from the left edge of the alley to the point on the alley directly below the intersection point of the ladders. Call b the distance from the right edge of the alley to the point on the alley directly below the intersection point of the ladders. From similar triangles we get:
p/x = a/(a+b)
p/y = b/(a+b)
Add the two equations:
p/x + p/y = a/(a+b) + b/(a+b)
py/xy + px/xy = (a+b)/(a+b)
p(x+y)/xy = 1
p = xy/x+y
1/p = x+y/xy
1/p = x/xy + y/xy
1/p = 1/y + 1/x
Thanks Scott for this observation.
Michael Shackleford, A.S.A.
| | | 152. | Ant and spider on a piece of wood problem
|   | | In a backyard lies a block of wood 9" by 9" by 22". The long edge of the board lies along a north/south direction. An ant is sitting on the south end of the board, half way up vertically, and 1" from the east edge. A spider is sitting on the north end of the board, half way up vertically, and 1" from the west edge. The spider can crawl at a rate of 1" per minute. The ant figures that it will take 1+22+8=31 minutes for the spider to reach him so he dozes off for a 30 minute nap. Just as the ant wakes up the spider kills him. By what route did the spider take to get to the ant in 30 minutes?  Answer
Answer Problem 152 AnswerVisualize the box folded out. The spider has to crawl 22"+1"+1"=24" vertically and 4.5"+9"+4.5"=18" horizontally. The total distance traveled is (24"2 + 18"2)1/2 =
(576" + 324")1/2 =
900"1/2 =
30". 
Thanks to Anil Rhemtulla for this problem. Michael Shackleford, ASA, March 11, 2000> | | | 4. | Ant and spider problem
|   | | An ant and a blind spider are on opposite corners of a cube. The ant is stationary and the spider moves at random from one corner to another along the edges only. What is the expected number of turns before the spider reaches the ant? Optional: Also solve for a square, octahedron, icosahedron, and dodecahedron.  Answer
Answer
Problem 4 Answer
Problem 4 Answer
The answer is 10.
If the spider started at a corner diagonally on the same face as
the ant the answer would be 9, and if the spider started at an
adjacent corner the answer would be 7.
Here are answers for other figures:
Square: 4
Octahedron: 6
Dodecahedron: 35
Icosahedon: 15
Michael Shackleford, A.S.A.
Solution
Problem 4 Solution
Let x=number of turns to reach ant from starting point.
Let y=number of turns to reach ant from diagonal corner on same face as
ant.
Let z=number of turns to reach ant from an adjacent corner to ant.
After one turn the spider will be on a diagonal corner of a common face as
the ant. So the mean number of turns from the x position is one more than
the mean number from the y position:
E(x)=1+E(y).
Once at a y position there is a 2/3 chance it will then move to a z
position, and a 1/3 chance back to an x position:
E(y)=(2/3)*(1+E(z))+(1/3)*(1+E(x)).
If the spider arrives at a z position there is a 1/3 chance it will move to
the ant, and a 2/3 chance it will move back to a y position:
E(z)=(1/3)*1+(2/3)*(1+E(y)).
With these three equations and three unknowns it is not difficult to solve
for E(x), E(y), and E(z).
Michael Shackleford, A.S.A.
| | | 206. | Ant on a rubber band problem
| | | Imagine an infinitely elastic rubber band that is 1 km. long unstretched. It expands at a rate of 1 km. per second. Next, imagine an ant at one end of the rubber band. At the moment the rubber band starts expanding the ant crawls towards the other end at a speed, relative to his current position, of 1 cm. per second. Will the ant ever reach the other end? If so, when?  Answer
Answer Problem 206 Answer
Question
Imagine an infinitely elastic rubber band that is 1 km. long unstretched. It expands at a rate of 1 km. per second.
Imagine an ant at one end of the rubber band. At the moment the rubber band starts expanding the ant crawls towards the other end at a speed, relative to his current position, of 1 cm. per second.
Will the ant ever reach the other end? If so, when?
Answer
Yes. The ant will reach the other end after e100,000 - 1 seconds.
Michael Shackleford, ASA — Dec. 10, 2010
Problem 206 Solution
Question
Imagine an infinitely elastic rubber band that is 1 km. long unstretched. It expands at a rate of 1 km. per second.
Imagine an ant at one end of the rubber band. At the moment the rubber band starts expanding the ant crawls towards the other end at a speed, relative to his current position, of 1 cm. per second.
Will the ant ever reach the other end? If so, when?
Solution #1
Let f(t)=distance traveled from origin at time t.
So f'(t)=speed of ant at time t.
f'(t)= 1 + 100,000×ratio of progress.
The ratio of progress is the distance the ant has covered divided by the length of the rubber band = f(t)/(100,000*(1+t))
So f'(t) = 1 + 100,000 * f(t)/(100,000*(1+t))
f'(t) = 1 + f(t)/(1+t)
So, for what f(t) is this true? Here is where you pretty much need to have some linear differential equations in your back pocket. What works is f(t)=(1+t) × ln(1+t)
Let g(t)=length of rubber band time t.
g(t)=100,000×(1+t)
The question is at what time t is f(t)=g(t)?
(1+t) × ln(1+t) = 100,000×(1+t)
ln(1+t) = 100,000
1+t = e100,000
t = e100,000-1
My thanks to Doc for solution #1.
Solution #2
The ratio of the rubber band the ant covers at time t is 1/[100000×(1+t)]. To help visualize this, think of the ant's position as your relative point of reference, and both ends of the rubber band moving away from the ant. So the ratio of progress is the ant's speed of 1 cm/sec compared to the total length of the rubber band at time t of 100,000×(t+t).
The question is, at what time T will the sum of the progress be 1?
Integral from 0 to T of 1/[100000×(1+t)] dt = 1
10-5×ln(1+t) from 0 to T = 1
10-5×(ln(1+T)-ln(0)) = 1
10-5×ln(T) = 1
ln(1+T)=100,000
1+T=e100,000
T=e100,000-1
My thanks to PapaChubby for solution #1.
General Answer
Let:
a = ant's speed.
b = rubber band's expansion speed.
c = initial length of rubber band.
Then the ant will get to the end in (c/b)×(eb/a-1) units of time.
Michael Shackleford, ASA — Dec. 6, 2010 | | | 195. | Average of the least of n random numbers from 0 to 1?
|   | | What is the average of the least of n random numbers from 0 to 1?  Answer
Answer
Problem 195 Answer
Problem 195 Answer
The answer is 1/(n+1).
Michael Shackleford, A.S.A.
Solution
Problem 195 Solution
Problem 195 Solution
In problem 194, we see the solution for the 2-number case is 1/3. The following shows the solution for the 3-number case is 1/4, and for the 4-number case is 1/5. Following the pattern, the solution for the n-number case is 1/(n+1).
If it isn't clear from the scan below, first I find the area of integration, and then multiply the expected average by the inverse of that area. In the 3-number case, x is the largest number, and ranges from 0 to 1. y is the second largest, and ranges from 0 to x. z is the smallest and ranges from 0 to y. Same concept in the 4-number case, but we start with w as the largest number.

Michael Shackleford, A.S.A.
| | | 194. | Average of the lesser of two random numbers from 0 to 1?
|  | | What is the average of the lesser of two random numbers from 0 to 1?  Answer
Answer
Problem 194 Answer
Problem 194 Answer
The answer is 1/3.
Michael Shackleford, A.S.A.
Solution
Problem 194 Solution
Problem 194 Solution
See the following scan. The reason for multiplying by 2, is the area of integration is 1/2, as shown by the shaded area. x is the larger of the two numbers, which can range from 0 to 1. y is the smaller number, which can range from 0 to x.
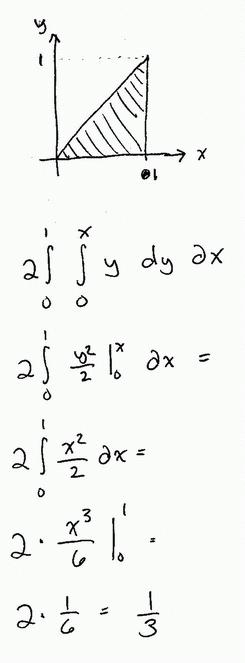
Michael Shackleford, A.S.A.
| | | 56. | Babies in the nursery problem
|   | | A baby is added to a hospital nursery. Before the baby was added there were two boys in the nursery and an uncounted number of girls. After the new baby is added a baby is selected at random among all the babys. The selected baby is a boy. What is the probability that the added baby was a girl?  Answer
Answer
Problem 56 Answer
Problem 56 Answer
The answer is 40%.
Michael Shackleford, A.S.A.
Solution
Problem 56 Solution
Problem 56 Solution
Bayes' Theorem:
Let events A1,...,Ak form a partition of the space
S such that Pr(Aj)>0 for j=1,...,k, and let B be any
event such that Pr(B)>0. Then for i=1,...,k,
Pr(Ai|B) = Pr(Ai)*Pr(B|Ai) / Sum for j=1 to k of
Pr(Aj)*Pr(B|Aj).
The source of this problem is the May 1997 issue of the Actuarial Review.
Applying this theorm:
B=boy selected
A1=boy added
A2=girl added
g=number of girls before baby is added.
Pr(A2|B) = (1/2)*(2/(3+g)) / [(1/2)*(2/(3+g)) + (1/2)*(3/(3+g))] = 0.4
Michael Shackleford, A.S.A.
| | | 24. | Baby bottle problem
|   | | You need to warm milk in a baby bottle from its initial temperature of 15 degrees centigrade to 25 degrees. You put the bottle in a pot of boiling water which stays at constant temperature of 100 degrees. The thickness and conductivity of the bottle are such that the initial rate of heat transfer is 85 degrees per minute. However heat transfer is proportional to the difference between the temperature of the milk and the water. How many minutes will it take to heat the bottle to 25 degrees?  Answer
Answer
Problem 24 Answer
Problem 24 Answer
ln(17/15) =~ 0.1252
The Wizard of Odds
Solution
Problem 24 Solution
Problem 24 Solution
dc/dt = 100-c
dc = 100-c dt
dc 1/(100-c) = dt
-ln(100-c) = t + K1
t = ln(K2) - ln(100-c) (where K1 = ln(K2)
t = ln(K2/(100-c))
When t=0 c=15 so K2 must be 85
t = ln(85/(100-c))
Solving for t when c=25:
t = ln(85/(100-25)) = ln(85/75) =~ ln(17/15) = 0.1252
The Wizard of Odds
| | | 19. | Balls and an urn problem #1
|   | | You have an urn with four balls of different colors. Randomly you draw two at a time, then painting the first ball to match the second. What is the expected number of drawings before all balls are the same color?  Answer
Answer
Problem 19 Answer
Problem 19 Answer
The answer is 9.
Michael Shackleford, A.S.A.
Solution
Problem 19 solution
Problem 19 Solution
Call the four colors 1,2,3, and 4.
After the first turn you will have a configuration like 1,1,2,3.
Call this configuration 1.
From configuration 1 if you draw a 1 on the first ball you will end
up with the same or similar configuration. The probability of this
happening is 1/2.
From configuration 1 if you draw a 3 or 4 first and then a 1 you
will have a configuration like 1,1,1,2. The probability of this
happening is 1/3. Call this new pattern configuration 2.
From configuration 1 if you draw a 3 or 4 first and then draw
the other non 1 you will have a configuration like 1,1,2,2. The
probability of this is 1/6. Call this new pattern configuration 3.
From configuration 2 you will end up with the same pattern with
probability 1/2, configuration 3 with probability 1/4, and ending
the experiment with probability 1/4.
From configuration 3 you will end up with the same thing with
probability 1/3, and with configuration 2 with probability 2/3.
From this information you can draw the following equations, where
a is the expected number of turns from equation 1, b from equation 2,
and c from equation 3:
- a=(a+1)/2 + (b+1)/3 + (c+1)/6
- b=(b+1)/2 + (1)/4 + (c+1)/4
- c=(c+1)/3 + (2/3)*(b+1)
Finally simple matrix algebra will show a=8. Considering the first
turn from the original condition to equation 1 the expected number of
turns is 9.
Michael Shackleford, A.S.A.
| | | 200. | Baseball playoffs question
|    | | Prior to 2013, in Major League Baseball, the American League had three divisions, the East and Central divisions with 5 teams each, and the West division with 4 teams. Four teams in the the league will make the playoffs, the three division leaders, and a wild card team. The wild card team is the team with the best record in the league, not including the three division leaders. Assuming all teams are equally good, what is the probability of a team in each division making the playoffs? Assume any ties are broken randomly. For extra credit, also do the National League, in which the East and West divisions have 5 teams, and the central division has 6 teams.  Answer
Answer
Problem 200 Answer
Problem 200 Answer
American East 27.492507%
American Central 27.492507%
American West 31.268731%
National East 25.934066%
National Central 23.443223%
National West 25.934066%
Michael Shackleford, ASA — Nov 26, 2008
Solution
Problem 200 Solution
Problem 200 Solution
Question
In Major League Baseball, the National League has three divisions, the East and Central divisions with 5 teams each, and the West division with 4 teams. Four teams in the National League will make the playoffs, the three division leaders, and a wild card team. The wild card team is the team with the best record in the league, not including the three division leaders. Assuming all teams are equally good, what is the probability of a team in each division making the playoffs? Assume any ties are broken randomly.
Solution
The difficult part of this question is determing the probability that the Wild Card team will fall in any given division. Let's consider the American League East first. There are six ways the wild card team could be in the American League East, as follows.
American League East has both first and second place teams in the entire American League. The probability of this is (5/14)×(4/13) = 10.9890%. American League East has both first and third place teams, but not the second, in the entire American League. The probability of this is (5/14)×(4/13)×(9/12) = 8.2418%. American League East has both second and third place teams, but not the first, in the entire American League. The probability of this is (5/14)×(4/13)×(9/12) = 8.2418%. American League East has both first and fourth place teams, in the entire American League, and the second and third place teams fall one each into the other two divisions. The probability of this is = (5/14)×(4/13)×((5/12)×(4/11)+(4/12)×(5/11)) = 3.3300%. American League East has both second and fourth place teams, in the entire American League, and the first and third place teams fall one each into the other two divisions. The probability of this is = (5/14)×(4/13)×((5/12)×(4/11)+(4/12)×(5/11)) = 3.3300%. American League East has both third and fourth place teams, in the entire American League, and the first and second place teams fall one each into the other two divisions. The probability of this is = (5/14)×(4/13)×((5/12)×(4/11)+(4/12)×(5/11)) = 3.3300%.
Add these probabilties together and you get 37.4625%. It is obvious the probability should be the same for the American League Central. The probability for the American League West thus has a probability of 100% - 2×37.4625% = 25.074925% of having the wild card team.
The probability any given team will be a division leader is 20% in the East and Central divisions, and 25% in the West division. These are also the probabilities for the wild card spot, given that it is in the same division. So, the probability that a team from the East or Central divisions makes the playoffs is 20% + 37.4625%×20% = 27.492500%. The probability that a team from the West division makes the playoffs is 25% + 25.074925%×25% = 31.268731%.
Extra Credit
The probability the National League East or West division will get the wild card is 29.670330% each, and 40.659341% for the Central division. The probability any given team in the East or West will make the playoffs is 25.934066%, and 23.443223% for Central.
Summary
American East 27.492507%
American Central 27.492507%
American West 31.268731%
National East 25.934066%
National Central 23.443223%
National West 25.934066%
Michael Shackleford, ASA — Nov 26, 2008
| | | 154. | Biased coin flipping problem #1
|   | | A loaded coin has probability of landing on heads of 0.6 and for tail 0.4. Winning bets on heads pay even money. With an initial fortune of $10 and betting $1 at a time what is the probability of eventual ruin assuming you kept playing until being ruined?  Answer
Answer
Problem 154 Answer
Problem 154 Answer
The answer is (2/3) 10 =~ 0.017342 .
This problem is from the March 2000 issue of The Actuary, published
by the Society of Actuaries.
Michael Shackleford, ASA - April 5, 2000
Solution
Problem 154 Solution
Problem 154 Solution
Let p i be the probability of ruin given a bankroll of $i.
p1 = .4 + .6*p2
p2 = .4*p1 + .6*p3
p3 = .4*p2 + .6*p4
p4 = .4*p3 + .6*p5
p5 = .4*p4 + .6*p6
.
.
.
Now sum the equations.
Sum for i=1 to infinity of pi = .4 + .4*(sum for i=1 to infinity of pi) + .6*(sum for i=2 to infinity of pi)
Sum for i=1 to infinity of pi = .4 + (sum for i=1 to infinity of pi) -.6*p1)
.6*p1=.4
p1=.4/.6 = 2/3
At this point you can use substitution to find that pi=(2/3)i.
So p10=(2/3)10=~0.017342
This problem is from the March 2000 issue of The Actuary, published
by the Society of Actuaries.
Michael Shackleford, ASA - April 5, 2000
| | | 155. | Biased coin flipping problem #2
|    | | Suppose before taking the first bet of the previous problem you consult your crystal ball which says you will eventually be ruined. Being a compulsive gambler you play anyway until ruin. What is the ratio of total heads to total flips?  Answer
Answer
Problem 155 Answer
Problem 155 Answer
The answer is 0.4 .
This problem is from the March 2000 issue of The Actuary, published
by the Society of Actuaries.
Michael Shackleford, ASA - April 5, 2000
Solution
Problem 155 Solution
Problem 155 Solution
Let p i be the probability that the first flip with bankroll of $i will be heads.
pi given eventual ruin = (pi&pr(ruin at $i+1))/pr(ruin at $i)=
.6*(.4/.6)11/(.4/.6)10 (see solution to problem 154 for probability of ruin) =
.6*(.4/.6) = 0.4
So the probability that any given flip will be heads is 0.4, thus the expected total flips
that are heads is also 0.4 .
This problem is from the March 2000 issue of The Actuary, published
by the Society of Actuaries.
Michael Shackleford, ASA - April 5, 2000
| | | 202. | Blue and Red Amoeba
|    | | Every generaion of red amoeba has a 5% chance of spawning 5 more red amoeba, a 10% chance of spawning 3 blue amoeba, a 1% chance of doing both, and a 84% chance of not spawning.
Every generaion of blue amoeba has a 3% chance of spawning 5 more blue amoeba, a 2% chance of spawning 10 red amoeba, a 1% chance of doing both, and a 94% chance of not spawning.
Your petri dish starts with one red amoeba. What is the expected number of red and blue amoeba observed before all amoeba die off?  Answer
Answer
Problem 202 Answer
Problem 202 Answer
Question
Every generaion of red amoeba has a 5% chance of spawning 5 more red amoeba, a 10% chance of spawning 3 blue amoeba, a 1% chance of doing both, and a 84% chance of not spawning.
Every generaion of blue amoeba has a 3% chance of spawning 5 more blue amoeba, a 2% chance of spawning 10 red amoeba, a 1% chance of doing both, and a 94% chance of not spawning.
Your petri dish starts with one red amoeba. What is the expected number of red and blue amoeba observed before all amoeba die off?
Answer
One red amoeba will spawn into 800/461 =~ 1.7354 on average.
One red amoeba will spawn into 330/461 =~ 0.7158 blue amoeba on average.
Michael Shackleford, ASA — Apr. 1, 2009
Solution
Problem 202 Solution
Problem 202 Solution
Question
Every generaion of red amoeba has a 5% chance of spawning 5 more red amoeba, a 10% chance of spawning 3 blue amoeba, a 1% chance of doing both, and a 84% chance of not spawning.
Every generaion of blue amoeba has a 3% chance of spawning 5 more blue amoeba, a 2% chance of spawning 10 red amoeba, a 1% chance of doing both, and a 94% chance of not spawning.
Your petri dish starts with one red amoeba. What is the expected number of red and blue amoeba observed before all amoeba die off?
Solution
Let r = expected number of red amoeba observed per initial red amoeba.
Let b = expected number of red amoeba observed per initial blue amoeba.
Next, from the first piece of information, "Every generaion of red amoeba has a 5% chance of spawning 5 more red amoeba, a 10% chance of spawning 3 blue amoeba, a 1% chance of doing both, and a 84% chance of not spawning," we can put in equation form:
r = 1 + 0.05×5×r + 0.1×3×b + 0.01×(5r+3b)
r = 1 + 0.25r + .3b + 0.05r + 0.03b
r = 1 + 0.3r + 0.33b
Next, from the second piece of information, "Every generaion of blue amoeba has a 3% chance of spawning 5 more blue amoeba, a 2% chance of spawning 10 red amoeba, a 1% chance of doing both, and a 94% chance of not spawning," we can put in equation form:
b = 0.03×5b + 0.02×10r + 0.01×(5b+10r)
b = 0.15b + 0.2r + .05b + 0.1r
b = 0.2b + 0.3r
Using basic algebra, we can solve for r and b , given the two equations, and get:
r = 800/461 =~ 1.7354
b = 300/461 =~ 0.6508
So, one initial red amoeba will spawn into 1.7354 on average. We also know that one blue amoea will spawn into 0.6508 red amoeba on average. However, that doesn't tell us how many blue amoeba a red amoeba will spawn into. To answer that question, let's redefine the variables as follows:
Let r = expected number of blue amoeba observed per initial red amoeba.
Let b = expected number of blue amoeba observed per initial blue amoeba.
Putting the initial conditions into equations:
r = 0.3r + 0.33b
b = 1 + 0.2b + 0.3r
Using algebra to solve the equations we get:
r = 330/461 =~ 0.7158
b = 700/461 =~ 1.5184
So, one red amoeba will spawn into 0.7158 blue amoeba on average.
Simulation
I did a random simulation of 74,016,000,000 initial states of one red amoeba. Following were the total counts observed:
Red amoeba: 128,445,045,020
Blue Amoeba: 52,983,662,357
That is an averoage of 1.735368637 red and 0.715840661 blue.
Michael Shackleford, ASA — Apr. 1, 2009
| | | 149. | Burried treasure problem
|   | | You find an old treasure map to the location of a buried treasure chest on a deserted island. The map states on this island are an oak tree, a palm tree, and a gallows. You are to start at the gallows, walk toward the palm tree while counting your steps. Then turn 90 degrees to the left and walk the same number of steps. At that spot drive a stake. Then walk from the gallows to the oak tree, again measuring your steps. When you get to the oak tree turn 90 degrees to the right and walk the same number of steps, then drive a stake at that spot. Then find the midpoint between the two stakes and dig.
When you get to the island you find the gallows are gone. Without digging at random is it possible to figure out the location of the treasure chest? If so where is it?  Answer
Answer
Problem 149 Answer
Problem 149 Answer
The treasure chest can be in one of two places. Find the midpoint of the two
trees and walk in either direction on the line perpendicular to the line that
contains both trees. Stop after walking half the distance between the two
trees and dig. If the treasue isn't there then walk the other direction from the
midpoint of the two trees and it must be there.
Thanks to the
Geometry Forum for this problem.
Michael Shackleford, ASA, October 21, 1999
Solution
Problem 149 Solution
Problem 149 Solution
Consider the oak tree to be at point (0,0), the palm tree to be at
(p,0), and the gallows to be at (x,y). The location of the first stake is
(p+y,p-x). The location of the second stake is (-y,x). The midpoint
is ((p+y-y)/2,(p-x-(-x))/2) = (p/2,p/2).
Thanks to the
Geometry Forum for this problem.
Michael Shackleford, ASA, October 21, 1999
| | | 110. | Cable in the field problem
|     | | There is a straight cable buried under a unit square field. You must dig one or more ditches to locate the buried cable. Where should you dig to guarantee finding the cable and to minimize digging? For example you could dig an X shape for total ditch length of 2*sqr(2) but there is a better answer.  Answer
Answer
Problem 110 Answer
Problem 110 Answer
Let the corners of the square be at (0,0),(1,0),(1,1), and (0,1).
The solution is to dig the following ditches:
- (0,0) to (x,x)
- (1,0) to (x,x)
- (0,1) to (x,x)
- (1/2,1/2) to (1,1)
Where x = (3-sqr(3))/6 =~ 0.2113248654
The total length of all ditches is aproximately 2.6389584338
I'd like to thank the
Macalester College Problems of the Week for this problem.
Michael Shackleford, A.S.A.
| | | 99. | Camel and grain problem
|  | | It is your task to deliever as much grain as possible from city A to city B. The cities are 1,000 miles apart. You initially have 10,000 pounds of grain. Your camel may carry up to 1,000 pounds and eats 1 pound of grain per mile traveled. You may leave grain along the way and return to it later. How much grain can you deliever to city B?  Answer
Answer
Problem 99 Answer
Problem 99 Answer
You can deliver 1399.77 pounds of grain.
Michael Shackleford, A.S.A., January 14, 1999
Solution
Problem 99 Solution
Problem 99 Solution
The way to deliver as much grain as possible is not not waste the camel's movement with
light loads. However moving heavy loads too small of a distance can often leave a small remainder
in the last trip, which is a waste of grain.
From the beginning you have enough grain to make 19 one-way trips to some cache point
along the way. The first question is, far out should you transport that grain? The answer is far enough so that you leave a cache somewhere of
9000 pounds of grain. Why 9000? Every cache point should have some amount of grain
evenly divisible by 1000. This way the camel can start out every trip with 1000 pounds, and not
have a remainder on the last trip. So you have 1000 pounds of grain to let the camel eat, divided by 19 one-way trips. 1000 pounds divided by 19 trips is 1000/19=~52.63 pounds, or 52.63 miles per trip. Each trip you will eat 52.63 miles along the way there, deposit
894.73 pounds of grain, and take back 52.63 pounds of grain to eat on the way home, except
the last trip in which you don't need to return. The total deposit works out to (10*894.73)+52.63 = 9000 pounds, as arranged. So you will be
able to cache 9000 pounds of grain 52.63 miles.
Next repeat the above but only allowing 17 one-way trips. 1000 divided by 17 is 1000/17 =~ 58.82 . So you will be able to cache 8000 pounds of grain 111.46 miles
from city A.
Below is a summary of the entire journey:
- Cache 9000 pounds over 19 one-way trips, moving 52.63 miles, or 52.63 miles from city A
- Cache 8000 pounds over 17 one-way trips, moving 58.82 miles, or 111.46 miles from city A
- Cache 7000 pounds over 15 one-way trips, moving 66.67 miles, or 178.12 miles from city A
- Cache 6000 pounds over 13 one-way trips, moving 76.92 miles, or 255.04 miles from city A
- Cache 5000 pounds over 11 one-way trips, moving 90.91 miles, or 345.95 miles from city A
- Cache 4000 pounds over 9 one-way trips, moving 111.11 miles, or 457.07 miles from city A
- Cache 3000 pounds over 7 one-way trips, moving 142.86 miles, or 599.92 miles from city A
- Cache 2000 pounds over 5 one-way trips, moving 200.00 miles, or 799.92 miles from city A
- Take 1000 pounds directly to city B, comsuming 200.08 pounds on the way, leaving 599.84 pounds
and take back 200.08 pounds to eat on the way back.
- Take the last 1000 pounds directly to city B, comsuming 200.08 pounds on the way, and
depositing an additional 799.92 pounds of grain, for a total deposit of 1399.77 pounds.
I would like to thank Scott Morris for this problem.
Michael Shackleford, A.S.A., January 14, 1999
| | | 64. | Cardiod problem
|    | | 
Two circles of radius one are adjancent at point (0,0). Let the center of the first circle be at point (-1,0). Label the point on the edge of the first circle at (0,0) x. The second circle is centered at (1,0). Rotate the first circle around the second, like a gear, keeping the second circle stationary. If you traced the path of point x as the first circle traveled around the second what would be the length of the path point x traced? The figure above shows the path in red.
Answer
Problem 64 Answer
Problem 64 Answer
The answer is 16.
Michael Shackleford, A.S.A.
Solution
Problem 64 Solution
Problem 64 Solution

Let a be the distance from the point (0,0) to a point on the figure (known as
a cardoid). Next consider the angle t formed from the points (-1,0), (0,0) and a at (0,0).
After working through the trigonomtry (this step is left to you) the length of a in terms of
t is 2*(1-cos(t)).
The formula for arc length is the integral of
( a2 + (da/dt)2 )1/2.
In this case it is the integral from 0 to 2*pi of:
( 4*(1-cos(t))2 + 4*sin2(t) )1/2. =
81/2 * (1 - cos(t))1/2.
After consulting a table of integrals we find that the integral of
(1 - cos(t))1/2 is -2*21/2*cos(t/2).
Taking the integral the answer works out to 16.
I'd like to thank Andrea for correcting an earlier mistake in my answer.
Michael Shackleford, A.S.A.
| | | 57. | Chessboard problem #1
|  | | 
Given an 2n by 2n chessboard, with one corner removed, show that you can cover it completely without overlapping or going off the board using only triominoes of the shape below.
Rotations are allowed.
Answer
Problem 57 Answer
Problem 57 Answer
For n=2 (4 by 4) you can cover the board like this:

For n=3 (8 by 8) use four sets of the 4 by 4 configuration. Use three of them
in such a way that the three extra squares form one extra triominoe, the fourth
one should have the extra square in the corner.:
For each additional n repeat the n-1 by n-1 configuration four times, rotating
in such as way as to create one extra triominoe.
Here is a nice graphic from Chris Johnson that explains the solution more clearly.
Thanks to Guy de Kindler
for this one.
Michael Shackleford, A.S.A.
| | | 58. | Chessboard problem #2
|  | | How many subsquares can you form on chessboard with n*n unit squares? Subsquares must be an integer squared.  Answer
Answer
Problem 58 Answer
Problem 58 Answer
The answer is n*(n+1)*(2n+1)/6.
Michael Shackleford, A.S.A.
Solution
Problem 58 solution
You can form n2 unit squares.
You can form (n-1)2 2 by 2 squares.
You can form (n-2)2 3 by 3 squares.
You can form (n-3)2 4 by 4 squares.
.
.
.
You can form 12 n by n square.
The sum of all these sums is n*(n+1)*(2n+1)/6
Thanks to Guy de Kindler
for this one.
Michael Shackleford, A.S.A.
| | | 9. | Chicken McNugget problem
|  | | At McDonalds you can order Chicken McNuggets in boxes of 6, 9, and 20. What is the largest number such that you can not order any combination of the above to achieve exactly the number you want?  Answer
Answer
Problem 9 Answer
Problem 9 Answer
The answer is 43.
Michael Shackleford, A.S.A.
Solution
For any desired number if it is divisible
by 3 it can easily be made with 6 and 9 packs,
except if the number is 3 itself. If you can't
use all six packs then use one 9 pack and you
can do the rest with six packs.
If the number is not divisible by 3 then
use one 20 pack. If the remaining number is
divisible by 3 then use the above method for
the rest.
If the number still isn't divisible by 3 use
a second 20 pack. The remainder must
be divisible by 3, in which case use the 6 and 9
packs as above.
The largest impossible number would be such that
you would have to subtract 20 twice to get a
remainder divisible by 3. However, you can't
make 3 itself with 6 and 9 packs. So the
largest impossible number is 2*20+3=43.
Michael Shackleford, A.S.A.
|
|