| 206. | Ant on a rubber band problem
| | | Imagine an infinitely elastic rubber band that is 1 km. long unstretched. It expands at a rate of 1 km. per second. Next, imagine an ant at one end of the rubber band. At the moment the rubber band starts expanding the ant crawls towards the other end at a speed, relative to his current position, of 1 cm. per second. Will the ant ever reach the other end? If so, when?  Answer
Answer Problem 206 Answer
Question
Imagine an infinitely elastic rubber band that is 1 km. long unstretched. It expands at a rate of 1 km. per second.
Imagine an ant at one end of the rubber band. At the moment the rubber band starts expanding the ant crawls towards the other end at a speed, relative to his current position, of 1 cm. per second.
Will the ant ever reach the other end? If so, when?
Answer
Yes. The ant will reach the other end after e100,000 - 1 seconds.
Michael Shackleford, ASA — Dec. 10, 2010
Problem 206 Solution
Question
Imagine an infinitely elastic rubber band that is 1 km. long unstretched. It expands at a rate of 1 km. per second.
Imagine an ant at one end of the rubber band. At the moment the rubber band starts expanding the ant crawls towards the other end at a speed, relative to his current position, of 1 cm. per second.
Will the ant ever reach the other end? If so, when?
Solution #1
Let f(t)=distance traveled from origin at time t.
So f'(t)=speed of ant at time t.
f'(t)= 1 + 100,000×ratio of progress.
The ratio of progress is the distance the ant has covered divided by the length of the rubber band = f(t)/(100,000*(1+t))
So f'(t) = 1 + 100,000 * f(t)/(100,000*(1+t))
f'(t) = 1 + f(t)/(1+t)
So, for what f(t) is this true? Here is where you pretty much need to have some linear differential equations in your back pocket. What works is f(t)=(1+t) × ln(1+t)
Let g(t)=length of rubber band time t.
g(t)=100,000×(1+t)
The question is at what time t is f(t)=g(t)?
(1+t) × ln(1+t) = 100,000×(1+t)
ln(1+t) = 100,000
1+t = e100,000
t = e100,000-1
My thanks to Doc for solution #1.
Solution #2
The ratio of the rubber band the ant covers at time t is 1/[100000×(1+t)]. To help visualize this, think of the ant's position as your relative point of reference, and both ends of the rubber band moving away from the ant. So the ratio of progress is the ant's speed of 1 cm/sec compared to the total length of the rubber band at time t of 100,000×(t+t).
The question is, at what time T will the sum of the progress be 1?
Integral from 0 to T of 1/[100000×(1+t)] dt = 1
10-5×ln(1+t) from 0 to T = 1
10-5×(ln(1+T)-ln(0)) = 1
10-5×ln(T) = 1
ln(1+T)=100,000
1+T=e100,000
T=e100,000-1
My thanks to PapaChubby for solution #1.
General Answer
Let:
a = ant's speed.
b = rubber band's expansion speed.
c = initial length of rubber band.
Then the ant will get to the end in (c/b)×(eb/a-1) units of time.
Michael Shackleford, ASA — Dec. 6, 2010 | | | 207. | Rubik's Cube problem
| | | Without taking it apart, how many permutations does a Rubik's Cube have?  Answer
Answer Problem 207 Answer
Question
Without taking it apart, how many permutations does a Rubik's Cube have?
8! × 12! × 38 × 212 = 519,024,039,293,878,000,000
Michael Shackleford, ASA — Apr. 9, 2011
Problem 207 Answer
Question
Without taking it apart, how many permutations does a Rubik's Cube have?
The six center faces of the cube are fixed. By turning the faces all you can do is rearrange the corners and edges. If you took the cube apart, then there would be 8!=40,320 ways to arrange the eight corners, without respect to the orientation of each piece. Likewise, there are 12!=479,001,600 ways to arrange the 12 edges without regard to orientation.
There are 3 ways each corner can be oriented, for a total of 38=6,561 corner orientations. Likewise there are two ways each edge piece can be oriented, for a total of 212=4,096 edge orientations.
So if we could take the cube apart, and rearrange the edge and corner groups, then there would be 8! × 12! × 38 × 212 = 519,024,039,293,878,000,000 possible permutations. However, not all of these permutations can be arrived at from the starting position by rotating the faces.
First, it is impossible to rotate just one corner and leave everything else the same. No combination of turns will achieve that. Basically, every action has to have a reaction. If you wish to rotate one corner, it would disturb the other pieces somehow. Likewise, it is impossible to flop just one edge piece. For these reasons, we have to divide the number of permutations by 3 × 2 = 6.
Second, it is impossible to switch two edge pieces without disturbing the rest of the cube. This is the hardest part of this answer to explain. All you can do with a Rubik's Cube is rotate one face at a time. Each movement rotates four edge pieces and four corner pieces for a total of eight pieces moved. A sequence of rotations can be represented by a number of piece movements divisible by 8. Often a sequence of moves will result in two movements canceling each other out. However, there will always be an even number of pieces moved with any sequence of rotations. To swap two edge pieces would be one movement, an odd number, which can not be achieved with the sum of any set of even numbers. Mathematicians would call this a parity problem. So we have to divide by another 2 because two edge pieces cannot be swapped without other pieces being disturbed.
So there are 3 × 2 × 2 = 12 possible groups of Rubik's Cube permutations. If you disassembled a Rubik's Cube and put it back together randomly, there is a 1 in 12 chance that it would be solvable. So the total number of permutations in a Rubik's Cube is 8! × 12! × 38 × 212 / 12 = 43,252,003,274,489,900,000. If you had seven billion monkeys, about the human world population, playing randomly with the Rubik's cube, at a rate of one rotation per second, a cube will pass through the solved position on average once every 196 years.
Michael Shackleford, ASA — Apr. 9, 2011
| | | 208. | Maximum volume of a cylinder problem
| | | A cylinder with an open top, has a surface area of S. What is the maximum volume it can hold?
Answer Problem 208 Answer
Question
A cylinder with an open top, has a surface area of S. What is the maximum volume it can hold?
The answer is [S2×(3×pi/S)1/2 - pi×(S/(3×pi))1/2]/(6*pi)
You may also wish to know that:
height=(S-pi×r2)/(2×pi×r)
radius=(S/(3×pi))1/2
Michael Shackleford, ASA — Feb. 7, 2012
Problem 208 Solution
Question
A cylinder with an open top, has a surface area of S. What is the maximum volume it can hold?
Let V be the volume of the cylinder.
Let S be the surface area of the can.
Let h be the height of the can.
Let r be the radius of the can.
V = pi×r 2×h
Let's express V as a function of r only.
S = pi×r 2 + 2×pi×r×h
Solving for h...
h = (S-pi×r 2)/(2×pi×r)
So...
V = ((S-pi×r 2)/(2×pi×r)) × pi×r 2
V = r×(S-pi×r 2)/2
Next, take the derivative of V and set equal to 0...
V- = (1/2)×(S×pi×r 2) = 0
S = 3×pi×r 2
r 2 = S/(3×pi)
r = (S/(3×pi)) 1/2
If we plug r in the equation for h, and then plug r and h into the equation for V we get...
V = [S 2×(3×pi/S) 1/2 - pi×(S/(3×pi)) 1/2]/(6×pi)
In the case of a surface area of 1, for example:
r = 0.325735
h = 0.325735
v = 0.108578
Michael Shackleford, ASA — Feb. 7, 2012
| | | 209. | Square wheel problem
| | | A square wheels rolls over a curved track such that the center of the square is always at the same height relative to the x-axis. If the square of side 2 makes a full revolution, how much horizontal distance will it cover?
Here are some equations you may find useful:
(cosh^-1(x))' = 1/sqrt(x^2 - 1)
cosh^-1(x) = ln(x +/- sqrt(x^2-1))
Answer
Problem 209 Answer
The answer is 8 × ln(2^0.5 + 1) =~ 7.051.
Michael Shackleford
Solution | | | 210. | What holds more water, a cup or cone?
| | | Given an equal amount of paper, which paper cup would hold more water, a cylinder or cone shape? Assume the cyliner is open on one end and optimal dimensions in both cases.
Answer Problem 210 Answer
Question
Given an equal amount of paper, which paper cup would hold more water, a cylinder or cone shape? Assume optimal dimensions in both cases.
The answer is the cone holds 7.4569932% more water than the cylinder.
Michael Shackleford, ASA — Feb. 7, 2012
Problem 210 Solution
Question
Given an equal amount of paper, which paper cup would hold more water, a cylinder or cone shape? Assume optimal dimensions in both cases.
We can see from problem 208 that a cylinder of surface area 1 can hold at most 0.108578.
We can see from problem 209 that a cone of surface area 1 can hold at most 0.116675.
The ratio of the volume of the cone to cylinder is 0.116675/0.108578 = 1.074570
The answer is the cone holds 7.4569932% more water than the cylinder.
Michael Shackleford, ASA — Feb. 7, 2012
| | | 211. | Hat and river problem
| | | Joe puts his canoe in the river and starts paddling upstream. After a mile his hat falls in the river. Ten minutes later he realizes his hat is missing and immediately paddles downstream to retrieve it. He catches up to it at the same place he launched his canoe in the first place. What is the speed of the river current?
Answer Problem 211 Answer
Question
Joe puts his canoe in the river and starts paddling upstream. After a mile his hat falls in the river. Ten minutes later he realizes his hat is missing and immediately paddles downstream to retrieve it. He catches up to it at the same place he launched his canoe in the first place.
What is the speed of the river current?
Answer
Three miles per hour.
Michael Shackleford, ASA — Feb. 7, 2012
Problem 211 Solution
Question
Joe puts his canoe in the river and starts paddling upstream. After a mile his hat falls in the river. Ten minutes later he realizes his hat is missing and immediately paddles downstream to retrieve it. He catches up to it at the same place he launched his canoe in the first place.
What is the speed of the river current?
Easy Solution
If Joe paddles upstream and them downstream the same amount of time in both directions then his effort paddling in both directions an equal amount of time would cancel out. In other words, he would end up in the same place if he floated the whole time.
We know he paddled upstream for ten minutes. So, after paddling downstream for another ten minutes he would end up in the same spot as he would had he floated for 20 minutes. We also know from the problem that in this same 20 minutes the hat floated one mile. So if the hat travels a mile in 20 minutes then it would travel three miles in an hour, for a speed of 3 m.ph..
Hard Solution
Let:
p=paddling speed in still water.
c=current of the water.
d=distance Joe paddled upstream since his hat fell out of the canoe.
Recall that distance = rate * time. Consider the unknown distance Joe went upstream since his hat fell out:
(1) d=(p-c)*(1/6)
This is because his net speed is the paddling speed less the current speed. We know he paddled without his hat upstream for 1/6 of an hour.
We're also given that it took the same time for the hat to float downriver a mile as it took for Joe to travel d miles upstream and 1+d miles downstream. Let's set up an equation, balancing for time.
(2) Time for hat to float one mile downstream = Time for Joe to travel d miles upstream + Time for Joe to travel 1+d times downstream.
Time for hat to float one mile downstream = one mile/rate of current = 1/c.
Time for Joe to travel d miles upstream = 1/6 (in hours), as provided in the question.
Time for Joe to travel 1+d times downstream = distance Joe traveled downstream / rate Joe traveled downstream = [1 + (1/6)*(p-c) ]/ (p+c).
The distance is the one mile the hat floated in the river + the (1/6)*(p-c) from equation (1). Joe’s speed going downstream is p+c, which is the sum of his paddling speed and current speed.
Now we’re ready to solve for equation (2)
1/c = (1/6) + [1 + (1/6)*(p-c) ]/ (p+c)
1/c = (1/6) + (6+p-c)/(6p+6c)
6/c = 1 + (6+p-c)/(p+c) Multiplying both sides by 6.
6/c = (p+c)/(p+c) + (6+p-c)/(p+c) Finding a common denominator
6/c = (6+2p)/(p+c)
6p + 6c = 6c + 2pc
6p = 2pc
3=c
So the current is 3 miles per hour.
Michael Shackleford, ASA — June 16, 2012
| | | 212. | Three logicans game #3
| | | Three logicians are on a game show. The host explains that each will be given his own black or white hat with 50% probability. Then each logician will be able to see the other logician's hats, but not his own. After the showing of the hats the host will separate the logicians and ask each of them the color of his own hat. Each logician may choose to not answer. The host will give each logician $1,000 if every answer submitted is correct, and at least one answer is submitted. Communication after the placing of the hats is not allowed. However, they are given time before the hat placing to devise a strategy. What strategy should they follow to maximize their odds of winning the prize, and what would be this probability of winning?
Answer Problem 212 Answer
Answer
If a logitian see both other hats are the same color then he should guess the opposite color.
The probability of winning is 75%.
Michael Shackleford, ASA — June 16, 2012
| | | 213. | Poker theory game #1
| | | - Players X and Y must each ante $1 into the pot.
- X and Y are each given a random number from a uniform distribution from 0 to 1.
- X may bet $1 or check.
- If X checks Y must check and the higher number will win the pot.
- If X bets, then Y may call or fold. If Y calls then the higher number will win the pot.
What is the optimal strategy for both players? Also, what is the expected win/loss of player X?
Answer Problem 213 Answer
Answer
Player X Strategy:
- 0.7 to 1.0: Bet
- 0.1 to 0.7: Check
- 0.0 to 0.1: Bet (bluff)
Player Y Strategy after a bet:
- 0.4 to 1.0: Call
- 0.0 to 0.4: Fold
The expected value of X is $0.10.
Michael Shackleford, ASA — Sept. 6, 2012
Problem 213 Solution
Solution
My method of solving this problem comes from The Mathematics of Poker by Bill Chen and Jerrod Ankenman.
First, we have to come up with a structure of the strategy for both players, without knowing yet the specifics. In this case, X should obviously raise above a certain point. Call it x2.
Second, X should also bluff below a certain point, call it x1.
With anything above x1 and below x2, X should check.
Y is the last to act, so there is no opportunity to bluff. He should simply fold below a certain point, and raise above it. Call that point y1.
The crux of their solution is to find indifference points where each player perceives the same expected value between two options. Let’s look at this problem as an example.
Next, we must decide which number will be greater, x1 or y1. It seems obvious to me that X will bluff only with a pretty low probability. Meanwhile, Y fold after a raise fairly often. So, based on common sense, I assume that x1
Now we're ready to get our hands dirty with some math. Let's start by finding an equation for x1. We do this by examining the possible outcomes for all possible values of Y, and how much X will win whether he bluffs or checks with exactly x1 points.
To be more specific,
- If Y has 1 to y1, then X will win -2 (or lose 2) if he bluffs and win -1 if he checks. The gain by bluffing is -1. The probability Y has a hand in this range is 1-x2. So, the expected increase in expected value by X bluffing with x1 is (1-y1)*-1 = y1-1.
- If Y has y1 to x1, then X will win 1 if he bluffs and win -1 if he checks. The gain by bluffing is 2. The probability Y has a hand in this range is y1-x1. So, the expected increase in expected value by X bluffing with x1 is (y1-x1)*2 = 2y1-2x1.
- If Y has x1 to 0, then X will win 1 if he bluffs and win 1 if he checks. In other words, X will win either way. So, the gain by bluffing is 0, and the expected value is also 0.
Here is a table the lays out the expected win by bluffing and checking if X has exactly X1, according to the value of Y1.
x1
| x1 |
| Y |
Bluff |
Check |
Difference |
Expected
Value |
| 1 to y1 | -2 | -1 | -1 | y1-1 |
| y1 to x1 | 1 | -1 | 2 | 2y1-2x1 |
| x1 to 0 | 1 | 1 | 0 | 0 |
The sum of the expected value column is -2x1+3y1-1. As stated above, we wish to set x1 to a value where the player is indifferent between bluffing and checking. So, we should set this expected value equation of the gain by bluff equal to zero. In other words, -2x1+3y1-1 = 0.
x2
Next, do the same thing, solving for x2. I will go right to the expected value table, which shows the expected value of raising, as opposed to checking, according to the value of Y.
| x2 |
| Y |
Bluff |
Check |
Difference |
Expected
Value |
| 1 to x2 | -2 | -1 | -1 | x2-1 |
| x2 to y1 | 2 | 1 | 1 | x2-y1 |
| y1 to 0 | 1 | 1 | 0 | 0 |
Setting the sum of the expected value column equal to 0 we get 2x2-y1-1=0.
y1
Next, we do a table for y1, showing the expected gain by calling, as opposed to checking, for every possible value of X.
| x2 |
| X |
Call |
Check |
Difference |
Expected
Value |
| 1 to x2 | -2 | -1 | -1 | x2-1 |
| x2 to y1 | -1 | -1 | 0 | 0 |
| y1 to x1 | 1 | 1 | 0 | 0 |
| x1 to 0 | 2 | -1 | 3 | 3x1 |
Setting the sum of the expected value column equal to 0 we get 3x1+x2-1=0.
Now we have three equations and three unknowns. Again they are:
-2x1+3y1-1=0
2x2-y1-1=0
3x1+x2-1=0
With a little matrix algebra we can solve for x1, x2, and y1 as follows:
x1=0.1
x2=0.7
y1=0.4
In other words, X should raise with less than 0.1 or more than 0.7, otherwise check. Assuming X raises, Y should fold with 0.4 or less, otherwise call.
The next question is what is the expected value for X if both players follow this strategy. To answer that question, let's consider how much X wins according to every significant grouping of X and Y.
| X Win Table |
| X |
Y |
| 0 to 0.1 | 0.1 to 0.4 | 0.4 to 0.7 | 0.7 to 1.0 |
| 0 to 0.1 | 1 | 1 | -2 | -2 |
| 0.1 to 0.4 | 1 | 0 | -1 | -1 |
| 0.4 to 0.7 | 1 | 1 | 0 | -1 |
| 0.7 to 1 | 1 | 1 | 2 | 0 |
Next, here is the probability of each combination of X and Y.
| Proability Table |
| X |
Y |
| 0 to 0.1 | 0.1 to 0.4 | 0.4 to 0.7 | 0.7 to 1.0 |
| 0 to 0.1 | 0.01 | 0.03 | 0.03 | 0.03 |
| 0.1 to 0.4 | 0.03 | 0.09 | 0.09 | 0.09 |
| 0.4 to 0.7 | 0.03 | 0.09 | 0.09 | 0.09 |
| 0.7 to 1 | 0.03 | 0.09 | 0.09 | 0.09 |
Finally, here is the expected value of the how much X will win for each combination, which is equal to the product of the win and the probability.
| X Return Table |
| X |
Y |
| 0 to 0.1 | 0.1 to 0.4 | 0.4 to 0.7 | 0.7 to 1.0 |
| 0 to 0.1 | 0.01 | 0.03 | -0.06 | -0.06 |
| 0.1 to 0.4 | 0.03 | 0 | -0.09 | -0.09 |
| 0.4 to 0.7 | 0.03 | 0.09 | 0 | -0.09 |
| 0.7 to 1 | 0.03 | 0.09 | 0.18 | 0 |
The sum of each cell in this table is 0.1. So, assuming the ante is $1 per player, X can expect to win 10 ¢ per hand.
Michael Shackleford, ASA — Sept. 6, 2012
| | | 214. | Three-player double-or-nothing game
| | | Three players play a game where the loser must double the money of both the other two players. They play this game three times and each player loses once. After three rounds each player has $24. How much did each player start with.
Answer Problem 214 Answer
Answer
The starting bankrolls were 12, 21, and 39.
Michael Shackleford, ASA — Sept. 28, 2012
Problem 214 Solution
Solution
Let's call the players P1, P2, and P3, and the starting bankrolls as follow:
Assume that P1 loses the first round. After he pays the winners the bankrolls we be:
Assume that P2 loses the second round. After he pays the winners the bankrolls we be:
- P1: 2x-2y-2z
- P2: -x+3y-z
- P3: 4z
Assume that P3 loses the third round. After he pays the winners the bankrolls we be:
- P1: 4x-4y-4z
- P2: -2x+6y-2z
- P3: -x-y+7z
All three of these sums must equal 24. So, we have three equations and three unknowns. That is enough to do a some simple matrix algebra to get x=39, Y=21, Z=12.
My thanks to WongBo for this problem.
Michael Shackleford, ASA — Sept. 28, 2012
| | | 215. | Poker theory game #2
| | | Same problem as number 213, except if X checks then Y can bet. Here are the full rules.
- Player X and Y each ante $1.
- Both are given a random number uniformly distributed from 0 to 1. The higher number wins.
- Player X may bet $1 or check.
- If player X checks then Y may check or bet.
- If player X bets then Y may call or fold.
- If player X checks, then Y bets, then X may call or fold.
What is the optimal strategy for both players? What is the expected value for X under mutual optimal strategy?
Answer Problem 215 Answer
My method of solving this problem comes from The Mathematics of Poker by Bill Chen and Jerrod Ankenman.
First, we have to come up with a structure of the strategy for both players, without knowing yet the specifics. Let's define some variables to this strategy as follows.
- x1 = If x has below x1 then he will bluff.
- x2 = If x checks, and then y bets, then x will fold with under x2, otherwise call.
- x3 = If x has above x3 then he will bet.
- y1 = If x checks, then y will bluff with under y1.
- y2 = If x bets, then y will fold with under y2, otherwise call.
- y3 = If x checks, then y will bet with over y3.
Here are the values for these indifference points.
x1 = 0.111111111
x2 = 0.333333333
x3 = 0.666666667
y1 = 0.166666667
y2 = 0.333333333
y3 = 0.500000000
Assuming the ante is $1 per player, x can expect to lose 5.55556 ¢ per hand.
Michael Shackleford — Nov. 1, 2012
Problem 215 Solution
Solution
My method of solving this problem comes from The Mathematics of Poker by Bill Chen and Jerrod Ankenman.
First, we have to come up with a structure of the strategy for both players, without knowing yet the specifics. Let's define some variables to this strategy as follows.
- x1 = If x has below x1 then he will bluff.
- x2 = If x checks, and then y bells, then x will fold with under x2, otherwise call.
- x3 = If x has above x3 then he will bet.
- y1 = If x checks, then y will bluff with under y1.
- y2 = If x bets, then y will fold with under y2, otherwise call.
- y3 = If x checks, then y will bet with over y3.
x1
Player x should be indifferent to checking and bluffing at x1. Let's take a look at how much x would win or lose both ways according to the value of y. The "difference" column shows the benefit to bluffing if x has exactly x1, and y has a value in the specified range. The "expected value" column shows the expected amount y can expect to win by bluffing, which is the product of the "difference" column and the probability that y has a value in the specified range.
| x1 |
| Y |
Bluff |
Check |
Difference |
Expected
Value |
| 1 to y2 | -2 | -1 | -1 | y2-1 |
| y2 to y1 | 1 | -1 | 2 | 2y2-2y1 |
| y1 to x1 | 1 | -1 | 2 | 2y1-2x1 |
| x1 to 0 | 1 | -1 | 2 | 2x1 |
The sum of the expected value column is 3y2-1. As stated above, we wish to set x1 to a value where the player is indifferent between bluffing and checking. So, we should set this expected value equation of the gain by bluff equal to zero. In other words, 3y2-1 = 0.
x2
Next, do the same thing, solving for x2. I will go right to the expected value table, which shows the expected value of calling, as opposed to foldling, according to the value of Y.
| x2 |
| Y |
Call |
Fold |
Difference |
Expected
Value |
| 1 to y3 | -2 | -1 | -1 | y3-1 |
| y3 to y1 | -1 | -1 | 0 | 0 |
| y1 to 0 | 2 | -1 | 3 | 3y1 |
Setting the sum of the expected value column equal to 0 we get 3y1+y3-1=0.
x3
Next, do the same thing, solving for x3. I will go right to the expected value table, which shows the expected value of raising, as opposed to checking, according to the value of Y.
| x3 |
| Y |
Raise |
Check |
Difference |
Expected
Value |
| 1 to x3 | -2 | -2 | 0 | 0 |
| x3 to y3 | 2 | 2 | 0 | 0 |
| y3 to y2 | 2 | 1 | 1 | y3-y2 |
| y2 to y1 | 1 | 1 | 0 | 0 |
| y1 to 0 | 1 | 2 | -1 | -y1 |
Setting the sum of the expected value column equal to 0 we get -y1-y2+y3=0.
y1
Next, we do a table for y1, showing the expected gain by bluffing, as opposed to checking, for every possible value of X.
| y1 |
| X |
Bluff |
Check |
Difference |
Expected
Value |
| 1 to x3 | -1 | -1 | 0 | 0 |
| x3 to x2 | -2 | -1 | -1 | x2-x3 |
| x2 to y1 | 1 | -1 | 2 | 2x2-2y1 |
| y1 to x1 | 1 | 1 | 0 | 0 |
| x1 to 0 | -1 | -1 | 0 | 0 |
Setting the sum of the expected value column equal to 0 we get 3x2-x3-2y1=0.
y2
Next, we do a table for y2, showing the expected gain by calling, as opposed to folding, for every possible value of X.
| y2 |
| X |
Call |
Fold |
Difference |
Expected
Value |
| 1 to x3 | -2 | -1 | -1 | x3-1 |
| x1 to 0 | 2 | -1 | 3 | 3x1 |
Setting the sum of the expected value column equal to 0 we get 3x1+x3-1=0.
y3
Next, we do a table for y3, showing the expected gain by raising, as opposed to checking, for every possible value of X.
| y3 |
| X |
Raise |
Check |
Difference |
Expected
Value |
| x3 to 1 | -2 | -2 | 0 | 0 |
| y3 to x3 | -2 | -1 | -1 | y3-x3 |
| x2 to y3 | 2 | 1 | 1 | y3-x2 |
| x1 to x2 | 1 | 1 | 0 | 0 |
| 0 to x1 | 2 | 2 | 0 | 0 |
Setting the sum of the expected value column equal to 0 we get -x2-x3+2y3=0.
Solving for x1, x2, x3, y1, y2, and y3.
Now we have six equations and six unknowns. Again they are:
3y2-1 = 0
3y1+y3-1 = 0
-y1-y2+y3 = 0
3x2-x3-2y1 = 0
3x1+x3-1 = 0
-x2-x3+2y3 = 0
Using matrix algebra, we should solve for the following matrix.
| 0 | 0 | 0 | 0 | 3 | 0 | 1 |
| 0 | 0 | 0 | 3 | 0 | 1 | 1 |
| 0 | 0 | 0 | -1 | -1 | 1 | 0 |
| 0 | 3 | -1 | -2 | 0 | 0 | 0 |
| 3 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | -1 | -1 | 0 | 0 | 2 | 0 |
Forgive me if I don't go through a matrix algebra lesson, and jump right to the solution, which is:
x1 = 0.111111111
x2 = 0.333333333
x3 = 0.666666667
y1 = 0.166666667
y2 = 0.333333333
y3 = 0.5
In other words, X should bluff with 0 to 0.111111, check with 0.111111 to 0.666667, and bet with 0.666667 to 1.0.
Assuming x bets or bluffs, then y should fold with 0 to 0.333333 and call with 0.333333 to 1.0.
If x checks, then y should bluff with 0.0 to 0.166667, check with 0.166667 to 0.500000, and bet with 0.500000 to 1.0.
Assuming x checks, and y bets, then x should fold with 0 to 0.333333 and call with 0.333333 to 1.0 (same strategy as y when forced to fold or call).
The next question is what is the expected value for X if both players follow this strategy. To answer that question, let's consider how much X wins according to every significant grouping of X and Y.
| X Win Table |
| X |
Y |
| 0 to x1 | x1 to y1 | y1 to x2 | x2 to y3 | y3 to x3 | x3 to 1 |
| 0 to x1 | 1 | 1 | 1 | -2 | -2 | -2 |
| x1 to y1 | -1 | -1 | -1 | -1 | -1 | -1 |
| y1 to x2 | -1 | -1 | 0 | -1 | -1 | -1 |
| x2 to y3 | 2 | 2 | 1 | 0 | -2 | -2 |
| y3 to x3 | 2 | 2 | 1 | 1 | 0 | -2 |
| x3 to 1 | 1 | 1 | 1 | 2 | 2 | 0 |
Next, here is the probability of each combination of X and Y.
| Proability Table |
| X |
Y |
| 0 to x1 | y1 to x1 | x2 to y1 | y3 to x2 | x3 to y3 | x3 to 1 | Total |
| 0 to x1 | 0.012346 | 0.006173 | 0.018519 | 0.018519 | 0.018519 | 0.037037 | 0.111111 |
| y1 to x1 | 0.006173 | 0.003086 | 0.009259 | 0.009259 | 0.009259 | 0.018519 | 0.055556 |
| x2 to y1 | 0.018519 | 0.009259 | 0.027778 | 0.027778 | 0.027778 | 0.055556 | 0.166667 |
| y3 to x2 | 0.018519 | 0.009259 | 0.027778 | 0.027778 | 0.027778 | 0.055556 | 0.166667 |
| x3 to y3 | 0.018519 | 0.009259 | 0.027778 | 0.027778 | 0.027778 | 0.055556 | 0.166667 |
| x3 to 1 | 0.037037 | 0.018519 | 0.055556 | 0.055556 | 0.055556 | 0.111111 | 0.333333 |
| Total | 0.111111 | 0.055556 | 0.166667 | 0.166667 | 0.166667 | 0.333333 | 1.000000 |
Finally, here is the expected value of the how much X will win for each combination, which is equal to the product of the win and the probability.
| X Return Table |
| X |
Y |
| 0 to x1 | y1 to x1 | x2 to y1 | y3 to x2 | x3 to y3 | 1 to x3 | Total |
| 0 to x1 | 0.012346 | 0.006173 | 0.018519 | -0.037037 | -0.037037 | -0.074074 | -0.111111 |
| y1 to x1 | -0.006173 | -0.003086 | -0.009259 | -0.009259 | -0.009259 | -0.018519 | -0.055556 |
| x2 to y1 | -0.018519 | -0.009259 | 0.000000 | -0.027778 | -0.027778 | -0.055556 | -0.138889 |
| y3 to x2 | 0.037037 | 0.018519 | 0.027778 | 0.000000 | -0.055556 | -0.111111 | -0.083333 |
| x3 to y3 | 0.037037 | 0.018519 | 0.027778 | 0.027778 | 0.000000 | -0.111111 | 0.000000 |
| 1 to x3 | 0.037037 | 0.018519 | 0.055556 | 0.111111 | 0.111111 | 0.000000 | 0.333333 |
| Total | 0.098765 | 0.049383 | 0.120370 | 0.064815 | -0.018519 | -0.370370 | -0.055556 |
The sum of each cell in this table is -0.055556. So, assuming the ante is $1 per player, X can expect to lose 5.55556 ¢ per hand.
Michael Shackleford, ASA — Nov. 1, 2012
| | | 216. | Expected rolls with two dice
| | | What is the expected number of rolls to attain every total from 2 to 12 with two six-sided dice?
Answer Problem 216 Answer
The answer is 61.217385.
Michael Shackleford, ASA — July 17, 2013
Problem 216 Solution
Solution
This question was asked at TwoPlusTwo.com, and was answered correctly by BruceZ. The following solution is the same method as that of BruceZ, who deserves proper credit. It is a difficult answer, so pay attention.
First, consider the expected number of rolls to obtain a total of two. The probability of a two is 1/36, so it would take 36 rolls on average to get the first 2. Next, consider the expected number of rolls to get both a two and three. We already know it will take 36 rolls, on average, to get the two. If the three is obtained while waiting for the two, then no additional rolls will be needed for the 3. However, if not, the dice will have to be rolled more to get the three.
The probability of a three is 1/18, so it would take on average 18 additional rolls to get the three, if the two came first. Given that there is 1 way to roll the two, and 2 ways to roll the three, the chances of the two being rolled first are 1/(1+2) = 1/3.
So, there is a 1/3 chance we'll need the extra 18 rolls to get the three. Thus, the expected number of rolls to get both a two and three are 36+(1/3)×18 = 42.
Next, consider how many more rolls you will need for a four as well. By the time you roll the two and three, if you didn't get a four yet, then you will have to roll the dice 12 more times, on average, to get one. This is because the probability of a four is 1/12.
What is the probability of getting the four before achieving the two and three? First, let's review a common rule of probability for when A and B are not mutually exclusive:
pr(A or B) = pr(A) + pr(B) - pr(A and B)
You subtract pr(A and B) because that contingency is double counted in pr(A) + pr(B). So,
pr(4 before 2 or 3) = pr(4 before 2) + pr(4 before 3) - pr(4 before 2 and 3) = (3/4)+(3/5)-(3/6) = 0.85.
The probability of not getting the four along the way to the two and three is 1.0 - 0.85 = 0.15. So, there is a 15% chance of needing the extra 12 rolls. Thus, the expected number of rolls to get a two, three, and four is 42 + 0.15×12 = 43.8.
Next, consider how many more rolls you will need for a five as well. By the time you roll the two to four, if you didn't get a five yet, then you will have to roll the dice 9 more times, on average, to get one, because the probability of a five is 4/36 = 1/9.
What is the probability of getting the five before achieving the two, three, or four? The general rule is:
pr (A or B or C) = pr(A) + pr(B) + pr(C) - pr(A and B) - pr(A and C) - pr(B and C) + pr(A and B and C)
So, pr(5 before 2 or 3 or 4) = pr(5 before 2)+pr(5 before 3)+pr(5 before 4)-pr(5 before 2 and 3)-pr(5 before 2 and 4)-pr(5 before 3 and 4)+pr(5 before 2, 3, and 4) = (4/5)+(4/6)+(4/7)-(4/7)-(4/8)-(4/9)+(4/10) = 83/90. The probability of not getting the four along the way to the two to four is 1 - 83/90 = 7/90. So, there is a 7.78% chance of needing the extra 7.2 rolls. Thus, the expected number of rolls to get a two, three, four, and five is 43.8 + (7/90)×9 = 44.5.
Continue with the same logic, for totals of six to twelve. The number of calculations required for finding the probability of getting the next number before it is needed as the last number roughly doubles each time. By the time you get to the twelve, you will have to do 1,023 calculations.
Here is the general rule for pr(A or B or C or ... or Z)
pr(A or B or C or ... or Z) =
pr(A) + pr(B) + ... + pr(Z)
- pr (A and B) - pr(A and C) - ... - pr(Y and Z) Subtract the probability of every combination of two events
+ pr (A and B and C) + pr(A and B and D) + ... + pr(X and Y and Z) Add the probability of every combination of three events
- pr (A and B and C and D) - pr(A and B and C and E) - ... - pr(W and X and Y and Z) Subtract the probability of every combination of four events
Then keep repeating, remembering to add probability for odd number events and to subtract probabilities for an even number of events. This obviously gets tedious for large numbers of possible events, practically necessitating a spreadsheet or computer program.
The following table shows the the expected number for each step along the way. For example, 36 to get a two, 42 to get a two and three. The lower right cell shows the expected number of rolls to get all 11 totals is 61.217385.
| Expected Number of Rolls Problem |
| Highest Number Needed |
Probability |
Expected Rolls if Needed |
Probability not Needed |
Probability Needed |
Expected Total Rolls |
| 2 | 0.027778 | 36.0 | 0.000000 | 1.000000 | 36.000000 |
| 3 | 0.055556 | 18.0 | 0.666667 | 0.333333 | 42.000000 |
| 4 | 0.083333 | 12.0 | 0.850000 | 0.150000 | 43.800000 |
| 5 | 0.111111 | 9.0 | 0.922222 | 0.077778 | 44.500000 |
| 6 | 0.138889 | 7.2 | 0.956044 | 0.043956 | 44.816484 |
| 7 | 0.166667 | 6.0 | 0.973646 | 0.026354 | 44.974607 |
| 8 | 0.138889 | 7.2 | 0.962994 | 0.037006 | 45.241049 |
| 9 | 0.111111 | 9.0 | 0.944827 | 0.055173 | 45.737607 |
| 10 | 0.083333 | 12.0 | 0.911570 | 0.088430 | 46.798765 |
| 11 | 0.055556 | 18.0 | 0.843824 | 0.156176 | 49.609939 |
| 12 | 0.027778 | 36.0 | 0.677571 | 0.322429 | 61.217385 |
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Michael Shackleford, ASA — July 17, 2013
| | | 217. | Solve epi*i
| | | Using Taylor's Formula, solve epi*i. hint.
Answer Problem 216 Answer
The answer is -1.
Michael Shackleford, ASA — Oct. 11, 2013
| | | 218. | Expected random numbers from [0,1] for the sum to exceed 1?
| | | What is the expected number of random numbers drawn from a uniform distribution from 0 to 1 so that the sum is greater than 1?
Answer Problem 218 Answer
The answer is e, or approximately 2.7182818.
Michael Shackleford, ASA — April 10, 2016
| | | 219. | 23 prisoners and two light switches problem
| | | There is a prison with 23 prisoners. The warden brings all the prisoners to a meeting and explains that he set up a room with two switches, labeled A and B. Each can be in an on or off position only. Starting the next day, the warden will pick a prisoner at random, with replacement, once per day. That prisoner will be led to the switches room. He must then switch one, and only one, switch of his choice.
When any member of the group declares "We have all been to the switch room," the warden will check his records to see if it is true. If it is true, then each prisoner will be set free immediately. If not, they will all be given the death penalty immediately.
The warden explains they can have the rest of the day to discuss strategy. Then they will all be separated and will never have a chance to communicate again, except via how they set the switches.
One final detail, the warden will set the switches in their initial state at random and not inform the prisoners beforehand of the initial setting.
Answer Problem 219 Answer
There are various solutions to the problem but most are variants of the one below. I believe my answer will get the prisoners released in the least number of expected days.
- The prisoner called to the switch room on the first day will be designated the leader. If switch A is in the up position, then he will flip in the down position. If it is already down, he will flip switch 2 (the dummy switch). He will start his running count of visits to 1.
- Starting with the second day, do the following:
- If a non-leader is called, and switch A is down position, and he has never fipped switch A, then he will flip switch A to the up position. This is the way to announce that one more person has visited the switch room.
- Otherwise, if a non-leader is called into the switch room, and any of the conditions are not met, then he should flip switch B.
- If the leader is called back into the room and switch A is in the up position it means a new prisoner has entered. The leader will flip A down and add one to his running count.
- If the leader is called back into the room and switch A is in the down position then it will mean no new prisoner has entered the room since the last time he was there. He will flip switch B.
- When the leader reaches a running count of 23, he can safely declare that everyone has been to the switch room at least once.
This method requires an average of 22*23 + sum for i=1 to 22 of 23/(23-i), which equals 591.8887 days.
Michael Shackleford, March 25, 2017
| | | 220. | Good Will Hunting problem
| | | Draw all homeomorphically irreducible trees of size n=10.
If this sounds familiar, it was the math problem posed in the movie Good Will Hunting, that Will solved. It was actually not so hard. Here is my attempt to put it in plain simple English:
Using only straight lines, draw all figures where the sum of intersections and dead ends equals 10. You may not have any closed loops. You may also not have two equivalent figures. Any intersection must have at least three paths leading from it. I'll give you a hint -- there are ten figures. In the movie, Will got only eight of them.
Answer Problem 220 Answer
Here is the answer, including two patterns Will didn't get.
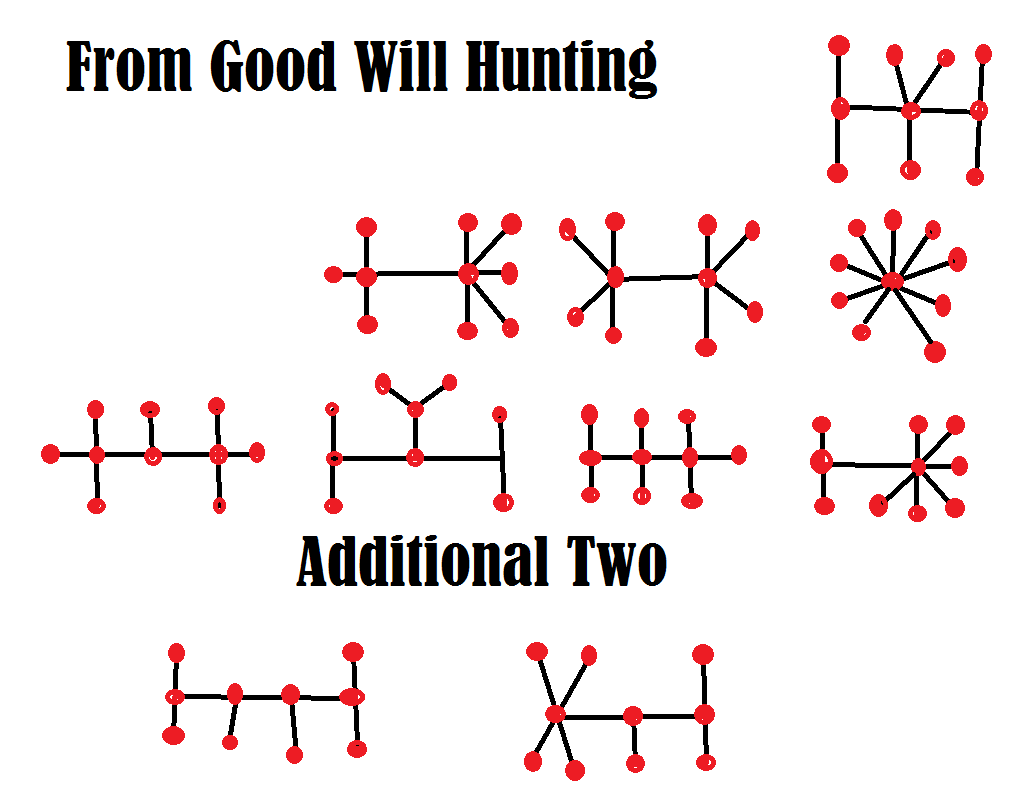 Michael Shackleford, April 5, 2017
Michael Shackleford, April 5, 2017
Problem 220 Solution
This solution is nothing very scientific but my attempt at a common sense answer.
- First, there is the case of just one intersection:
- Second, let's consider all the cases of two intersection points.
Let's start with the case of two nodes on one side. Considering both intersection points, and the two nodes on one side, there are six nodes left for the other side:
- Next, move a node from the side with six to the side with two, for a 3-5 split:
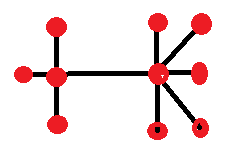
- Next, move a node from the side with five to the side with three, for a 4-4 split:
- Third, let's consider all the cases of three intersection points.
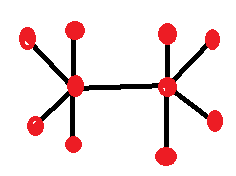
Let's start with the case of two nodes off one side. In the middle we can have just one node, since it has two intersection lines braching off of it. Consider the three intersections and three nodes, there are four nodes left for the other end:
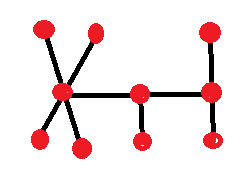
- Next, move a node from the side with four to the other end with only two:
- Next, move a node from either side to the middle:
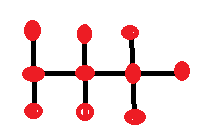
- Next, move a node from the other side (that still has three nodes) to the middle:
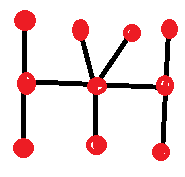
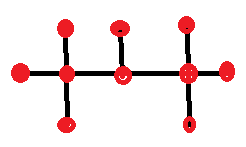
- Fourth, let's consider all the cases of four intersection points in a row.
Considering the two ends must have at least two nodes and the middle two must have at least one each, and the four intersection points themselves, we've already spoken for all ten points:
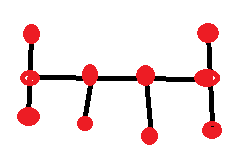
- Fifth, let's consider all the cases of four intersection points where there is one in the middle and three other branching off.
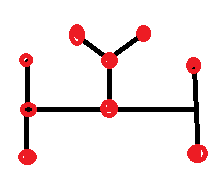
We've already spoken for four intersection points and each must have at least two nodes branching off, so we've already spoken for all 4+6=10 nodes:
Here is the full answer:
 Michael Shackleford, ASA — April 5, 2017
Michael Shackleford, ASA — April 5, 2017
| | | 221. | 25 horses problem
| | | You have 25 horses and a track that can race five horses at a time. The only thing you learn from each race is the winning order, from 1 to 5. You don't have a watch. Each horse always runs at its own constant speed. What is the least number of races required to determine the fastest three horses in order and how should it be done?
Answer Problem 221 Answer
The answer is 7.
Michael Shackleford, June 11, 2017
Problem 221 Solution
- Divide the 25 horses into five groups of five.
- Races 1-5: Race each group and note the top three horses, in order. Call these the heats.
- Race 6: Race the winner of each race from step 2. The winner of this race will be the fastest horse.
- Race 7: Race the the following five horses:
- Second and third place horses from race 6.
- The two horses from the group of five second place horses from step 1 that finished second in its heat to the winning two horses in race 6.
- The horse from the third place group that finished third in its heat to the winning horse in race 6.
There is a good explanation at A Collection of Quant Riddles With Answers of why this solution works.
Michael Shackleford, ASA — April 5, 2017
| | | 222. | Eight pieces of bread problem
| | | Two men sit down to have dinner. One contributed three loaves of bread and the other five. As they were about to start eating, a third man came along, who asked to join. They said "yes," and all three ate until the eight loaves were gone. As the third man was leaving he reached into his pocket and produced eight coins. He left them on the table for the two other men to split as they saw fit. What is a fair way to divide the eight coins?
Answer Problem 222 Answer
The man who contributed five loaves should get seven coins and the man who contributed three loaves should get one coin.
Michael Shackleford, July 3, 2017
Problem 222 Solution
Think about who contributed what to what the third man ate. Assuming each man ate the same amount, each ate 8/3 loaves. The man who contributed 5 loaves ate 8/3 of them, leaving 7/3 loaves to the third man. The man who contributed 3 loaves ate 8/3 of them, leaving 1/3 loaves to the third man.
So, of the 8/3 loaves eaten by the third man, 7/3 were from the man with five loaves and 1/3 from the man with three loaves. Thus split the coins according to whose bread you ate -- 7 coins to the man with five loaves and one coin to the man with three loaves.
Michael Shackleford, July 3, 2017
| | | 223. | Cylinder in a sphere problem #1
| | | What is the radius of the cylinder of maximum volume, which can be inscribed in a unit sphere?
Answer Problem 223 Answer
The radius which achieves the maximum volume of the cylinder is (2/3)^0.5 =~ 0.816496581.
Michael Shackleford, July 3, 2017
Problem 223 Solution
Call the radius of the cylinder 1. The distance from the center of the clinder to the edge is 1, because it is in a unit sphere. By phythagerous, we know the height of the cylinder must be (1-r^2)^0.5.
The volume of the clinder V is equal to pi*r^2*(1-r^2)^0.5.
Take the derivative and set it equal to zero:
pi*[2r*(1-r^2)^0.5 - r^3*(1-r^2)^-0.5] = 0.
2r*(1-r^2) = r^3
2/3 = r^2
r = (2/3)^0.5 =~ 0.816496581. The radius which achieves the maximum volume of the cylinder is (2/3)^0.5 .
The volume of said cylinder is 2*pi*sqrt(3)/9 =~ 1.209199576.
Michael Shackleford, July 3, 2017
| | | 224. | Cooling beer problem
| | | A refrigerator is kept at a constant temperature of 5 degrees.
A can of beer is placed in it with initial temperature of 25 degrees.
In one hour it cools to 15 degrees.
Assume that that the penguin that lives in the refrigerator not only turns the light on and off when you open the door but shakes the beer so that it maintains a constant temperature (and explodes in your face when you open it).
Hint: The rate of heat transfer is proportional to the difference between the temperature of object to the ambient temperature.
How long will it take to cool the beer to 5.1 degrees from the time it is placed inside the refrigerator?
Answer Problem 224 Answer
ln(200)/ln(2) =~ 7.6439 hours.
Michael Shackleford, July 4, 2017
Problem 224 Solution
Let: <
t = time (in hours) since beer was put in the refigerator.
T = temperature
k = constant of heat transfer
C = constant of integreation
We're given than Dt/dt = -k(T-5). It is negative because the beer can only decrease in temperature.
Dt = -k(T-5) dt
dt = -1/k(T-5) Dt
Integrate both sides:
t + C = -(1/k)*ln(T-5)
We're given that the temperature of the beer is 25 at t=0, so plug that in:
C = -(1/k)*ln(20)
We're also given that the temperature of the beer is 15 at t=1, so plug that in:
1 + C = -(1/k)*ln(10)
We have two equations and two unknowns so we can solve for k and C:
k = ln(2)
C = -ln(20)/ln(2)
So, the equation for time and temperature is:
t = ln(20)/ln(2) - ln(T-5)/ln(2)
So, if T=5.1, then
t = ln(20)/ln(2) - ln(0.1)/ln(2) = [ln(20) - ln(0.1)]/ln(2) = ln(200)/ln(2) =~ 7.6439 hours.
Michael Shackleford, July 4, 2017
| | | 225. | Poker theory game #3
| | | Consider a game with the following rules:
- A random number generator provides random numbers between 0 and 1 uniformly distributed.
- Two players each get a separate number. Each player can see his own number only.
- Player 1 may keep his initial number or swap for a new random number.
- Player 2, knowing player 1's action, has the same option to keep his original number or swap for a new one.
- Player with the higher number wins.
Answer the following questions about the game: - At what number is player 1 indifferent to standing and switching?
- Assuming player 1 switches, at what number should player 2 be indifferent to standing and switching?
- Assuming player 1 stands, at what number should player 2 be indifferent to standing and switching?
- Assuming optimal strategy by both players, what is the probability player 1 will win?
Answer Problem 225 Answer
- Player 1 is indifferent between standing and switching at (1/6)×(81+3×9211/2)1/3+(81-3×211/2)1/3 = 0.567364*.
- If player 1 hits, player 2 is indifferent between standing and switching at 0.5.
- If player 1 stands, player 2 is indifferent between standing and switching at 0.660951**.
- Assuming optimal strategy by bother players, the probability player 1 wins is 0.494333***.
* This is the solution to the equation 4x 3 + 4x - 3 = 0.
** This is the solution to the equation 3/(8x).
*** This is the solution to the equation (1/12) + (1/96)×(2763×(921) 1/3 - 19657) 1/3 - (2763×(921) 1/3 + 19657)) 1/3
Michael Shackleford, Nov. 19, 2017
Problem 225 Answer
There is some Nash equilibrium to be found between the two players. Let:
- Player 1 = player to act first.
- Player 2 = player to act second.
- x = Point at which player 1 is indifferent to standing and switching.
- y = Point at which player 2 is indifferent to standing and switching, assuming player 1 stood.
It should be obvious that y>x. If player 1 stood, player 2 knows that player 1 has a strong card, so he needs to be more aggressive to beat it. This is where positional advantage comes in. If this isn't obvious to you, then you probably should be attempting an easier problem.
First, let's calculate the probability of winning by standing.
- It is easy to see that the probability a given number x beats a random number is x.
- If player 2 has y or less, then the probability of player 1 winning is x.
- If player 2 has y or more, then the probability of player 1 winning is 0, since y>x.
- Taking the dot prodoct of the possible values for player 2 and the probability of player 1 winning by standing, the probability of winning by standing is xy.
Second, let's calculate the probability of winning by switching.
- It is easy to see that if player 1 switches, then player 2 will be indifferent to standing and switching at 0.5.
- If player 2 has 0.5 or less, then the probability of player 1 winning is 0.5, since both will have switched to a random card.
- If player 2 has 0.5 or more, then the probability of player 1 winning is 0.25. This can be found using geometry or integral calculus by looking at proption of the area player 1 wins over the area bounded by values of 0 to 1 for player 1 and 0.5 to 1 for player 2. Player 1 wins over 1/4 of that area.
- Taking the dot prodoct of the possible values for player 2 and the probability of player 1 winning by switching, the probability of winning by switching is 3/8.
Setting the expected value of standing and switching equal, we get xy = 3/8.
Next, solve for y using the same method. Forgive me if I don't through the details this time. Again, using simple geometry or integral calculus, you'll find the probability of player 2 winning by standing at y is (y-x)/(1-x). By the same method, the probability of player 2 winning by switching at y is [(1-x)2/2]/(1-x).
Setting the two equations equal and doing some algebra we get x2 - 2y + 1 = 0.
We now have two equations and two unknowns. With some simple algebra to solve for x we get to x3 + x -0.75 = 0. Using one of many cubic equaton solvers on the Internet, we find 0.567364. So, that is the value x is indifferent between standing and switching.
Putting that into xy=3/8, we solve for y as 0.660951.
Finally, find the probability of all four combinations of x and y standing and swithcing and the probability x wins for each one and take the dot product. The following table gives more details. The bottom right cell shows the probability player 1 wins is 0.494333.
| Player 1 |
Player 2 |
Probability |
Player 1
Action |
Player 2
Action |
Probability
Player 1 Wins |
Expected Value
Player 1 Wins |
| 0 to x | 0 to 0.5 | 0.283682 | switch | switch | 0.500000 | 0.141841 |
| 0 to x | 0.5 to 1 | 0.283682 | switch | stay | 0.250000 | 0.070921 |
| x to 1 | 0 to y | 0.285951 | stay | switch | 0.783682 | 0.224095 |
| x to 1 | y to 1 | 0.146685 | stay | stay | 0.391841 | 0.057477 |
| Total | | 1.000000 | | | | 0.494333 |
Final answers:
- Player 1 is indifferent between standing and switching at 0.567364.
- If player 1 hits, player 2 is indifferent between standing and switching at 0.5.
- If player 1 stands, player 2 is indifferent between standing and switching at 0.660951.
- Assuming optimal strategy by bother players, the probability player 1 wins is 0.494333.
Michael Shackleford, Nov. 19, 2017
| | | 226. | Poker theory game #4
| | | Consider a game with the following rules:
- A random number generator provides random numbers between 0 and 1 uniformly distributed.
- Both players bet $1 to start.
- Two players each get a separate number. Each player can see his own number only.
- Player 1 may keep his initial number or swap for a new random number. If player 1 swaps, both players must bet an additional $1.
- Player 2, NOT knowing player 1's action, has the same option to keep his original number or swap for a new one.
- Player with the higher number wins. The winner keeps all money bet
Answer the following questions about the game: - At what number is player 1 indifferent to standing and switching?
- At what number should player 2 be indifferent to standing and switching?
- Assuming optimal strategy by both players, how much can player 1 expect to win or lose?
Answer Problem 226 Answer
- Player 1 is indifferent between standing and switching at 0.456260889.
- Player 2 is indifferent between standing and switching at 0.554423955.
- Assuming optimal strategy by bother players, the expected loss of player is -0.13162138 dollars.
My thanks to Joe Shipman for his help with this problem.
Michael Shackleford, Nov. 22, 2017
Problem 226 Solution
There is some Nash equilibrium to be found between the two players. Let:
- Player 1 = player to act first.
- Player 2 = player to act second.
- x = Point at which player 1 is indifferent to standing and switching.
- y = Point at which player 2 is indifferent to standing and switching.
To begin, we must accept that y>x. Player 1 is going to be conservative about switching because he has to double his bet if he does. So, with a number around 0.5 he is better off to cut his losses and stick with it rather than double his bet and go against player 2 with a random card. Meanwhile, player 2 can be more aggressive because he can switch for free. With a number around 0.5, player 2 is apt to switch because he knows player 1 will have a number with an average over 0.5, because player 1 had the opportunity to switch out of the a bad number.
First, let's find x. We do so by finding the value of x where the expected value of standing and switching are equal.
At x, the expected value of standing is y*(2x-1)-(1-x). The expected value of switching at x is -2*y*(1-y).
Setting the two values equal to each other we get :
(1) 2*y^2 - 2xy - 2y + 1 = 0.
Second, let's find y. We do so by finding the value of y where the expected value of standing and switching are equal.
At y, the expected value of standing is x*(2*(2y -1)) + y - x - (1-y). The expected value of switching at x is -2x*(1 - x).
Setting the two values equal to each other we get:
(2) x^2 - 2y - 4xy +2x + 1 = 0.
We now have two equations and two unknowns. We can rewrite equation (1) as:
(3) x = y - 1 + 1/(2y).
Substituting equation (3) into (2) gives us:
(4) (2y^2 - 2y + 1)^2 - 2y*(4y^2) - 8y^2*(2y^2 - 2y + 1) + 4y*(2y^2 - 2y + 1) + 4y^2 = 0
After a lot of algebra, that reduces to:
(5) 12^4 - 8y^3 - 4y^2 - 1 = 0
You can use a four-order calculator to solve for y as 0.554423955.
You can plug that into equation (3) to get x = 0.456260889.
Finally, find the probability of all four combinations of x and y standing and swithcing and the probability x wins for each one and take the dot product. The following table gives more details. The bottom right cell shows player 1 can expect to lose 0.131621 dollars.
| Player 1 |
Player 2 |
Probability |
Player 1
Action |
Player 2
Action |
Probability
Player 1 Wins |
Expected Return
Player 1 |
Expected Value
Player 1 |
| Player 1 | Player 2 | Probability | Player 1 Action | Player 2 Action | Probability Player 1 Wins | ER player 1 | EV player 1 |
| 0 to x | 0 to y | 0.252962 | switch | switch | 0.500000 | 0.000000 | 0.000000 |
| 0 to x | y to 1 | 0.203299 | switch | stay | 0.222788 | -1.108848 | -0.225428 |
| x to 1 | 0 to y | 0.301462 | stay | switch | 0.728130 | 0.456261 | 0.137545 |
| x to 1 | y to 1 | 0.242277 | stay | stay | 0.409733 | -0.180533 | -0.043739 |
| Total | | 1.000000 | | | | | -0.131621 |
Final answers:
- Player 1 is indifferent between standing and switching at 0.456260889.
- Player 2 is indifferent between standing and switching at 0.554423955.
- Assuming optimal strategy by bother players, the expected loss of player is -0.13162138 dollars.
My thanks to Joe Shipman for his help with this problem.
Michael Shackleford, Nov. 22, 2017
| | | 227. | Two ferries problem
| | | Two ferries depart at right angles from opposite shores of a river. Each ferry travels at a consistent speed, although one is faster than the other. The pass each other 700 meters from the nearest shore. Upon reaching the other side, each spends 10 minutes docked. On the return trip they pass each other 400 meters from the opposite shore.
How wide is the river?
Answer Problem 227 Answer
The answer is 1700 meters.
Michael Shackleford, Nov. 28, 2017
Problem 227 Solution
Solution #1
Let's call x the distance between the two meetings points.
We can ignore the 10 minutes each spends turning around and assume the turn around instantly. This is simply obvious.
At the first meeting, the two boats combined would have traveled the width of the river.
At the second meeting, the two boats combined would have traveled three times the width of the river.
Since both boats travel at a consistent speed, both boats would have traveled three times as far at the second meeting as the first.
Let's solve for x looking at the fast boat.
3 × (time traveled until first meeting) = (time traveled until second meeting).
3 × (400+x) = 1800 + 2x.
x = 600.
So the total width of the river is 400+600+700 = 1700 meters.
Solution #2
Let's call:
- x = the distance between the two meetings points.
- f = speed of the fast ferry.
- s = speed of the slow ferry.
- t1 = time of first time ferries cross in the river.
- t2 = time of second time ferries cross in the river.
We can ignore the 10 minutes each spends turning around and assume the turn around instantly. This is simply obvious.
We all know that distance = rate × time. Let's express this equality at the first meeting for both ferries.
- Fast ferry: x + 400 = f * t1
- Slow ferry: 700 = s * t1
To reorder the above two equations:
- Fast ferry: t1 = (x+400)/f
- Slow ferry: t1 = 700/s
Those two expressions are equal:
t1 = (x+400)/f = t1 = 700/s
Let's express the distance=rate*time equality at the second meeting for both ferries.
- Fast ferry: 2x + 1800 = f * t2
- Slow ferry: x + 1500 = s * t2
To reorder the above two equations:
- Fast ferry: t2 = (2x+1800)/f
- Slow ferry: t2 = (x+1500)/s
Those two expressions are equal:
t2 = (2x+1800)/f = t1 = (x+1500)/s
It would seem we have two equations and three unknowns. However, we don't have to actually solve for f and s. We can express the the ratio f/s two ways, as follows:
f/s = (x+400)/700 = (1800+2x)/(1500+x).
Cross multiply to get:
x2 + 500x - 660000.
The quadratic formula easily gives us x=600. So the whole river is 700+600+400 = 1700 meters wide.
My thanks to Marvin Gardener, which can be found as problem 11 (with slightly different distances) in his book My Best Mathematical and Logic Puzzles.
Michael Shackleford, Nov. 28, 2017
| | | 228. | Cylinder in a sphere problem #2
| | | A drill drills through a section of a sphere of radius r right throuh the middle, leaving a hole 6" long. What is the volume of the remaining part of the sphere as a function of r?
Answer Problem 228 Answer
The answer is 36 × pi.
Michael Shackleford, Dec. 1, 2017
Problem 228 Solution
Let r = radius of the sphere.
To find the volume of the sphere left after you drive the hole through, consider the sphere centered at (0,0). Then find the volume of the part of the sphere ranging in x value from -3 to +3. Then we'll subtract out the area of the cylinder in the middle that the drill removed.
The area of the sphere from x = -3 to +3 equals:
Integral from -3 to +3 of (pi * (r^2-x^2)) dx =
pi * (r^2 * x - x^3/3) from -3 to 3 =
pi * (3r^2 - 9 + 3r^2 - 9) =
pi * (6r^2 - 18)
The volume of the missing cylinder is 6*pi*(r^2 - 9)
So, the volume of the part that is left is pi * (6r^2 - 18) - 6*pi*(r^2 - 9) =
36 * pi
So, it makes no difference what the radius of the sphere is, there will 36*pi left over after drilling through it.
Michael Shackleford, Dec. 1, 2017
| | | 229. | Flight around the world problem
| | | An island has a fleet of identical airplanes. Each plane can hold enough fuel to make it half way around the earth. The planes can refuel each other mid-flight. There is an unlimited supply of fuel on the island. Assuming no time or fuel lost in refueling or making a u-turn, what is the fewest number of airplanes needed to fly around the earth and how can it be done such that all planes must return safely to the island?
Answer Problem 229 Answer
The around the world flight can be accomplished with as few as three planes.
Michael Shackleford, Dec. 3, 2017
Problem 229 Solution
The around the world flight can be accomplished with only three planes.
The following table shows how it can be done. I'm sure there are variations of this that will also work. The time column is relative to the time required to fly around the earth non-stop. Fuel remaining is relative to a full tank. So a value of 1 would be full and 0 would be empty. The location is relative to a 360-degree circle, starting at the 0 point.
| Time | Fuel | Location |
Comment |
| A | B | C | A | B | C |
| 0.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0 | 0.0 | 0.0 | A, B, and C depart clockwise |
| 0.0625 | 0.8750 | 0.8750 | 0.8750 | 22.5 | 22.5 | 22.5 | C transfers 1/8 tank to A and B |
| 0.0625 | 1.0000 | 1.0000 | 0.6250 | 22.5 | 22.5 | 22.5 | C turns back |
| 0.1250 | 0.8750 | 0.8750 | 0.5000 | 45.0 | 45.0 | 0.0 | C refuels |
| 0.1250 | 0.8750 | 0.8750 | 1.0000 | 45.0 | 45.0 | 0.0 | C leaves |
| 0.2500 | 0.6250 | 0.6250 | 0.7500 | 90.0 | 90.0 | 45.0 | B refuels A |
| 0.2500 | 1.0000 | 0.2500 | 0.7500 | 90.0 | 90.0 | 45.0 | B turns back |
| 0.3125 | 0.8750 | 0.1250 | 0.6250 | 112.5 | 67.5 | 67.5 | C refuels B with a quarter tank |
| 0.3125 | 0.8750 | 0.3750 | 0.3750 | 112.5 | 67.5 | 67.5 | C turns back |
| 0.5000 | 0.5000 | 0.0000 | 0.0000 | 180.0 | 0.0 | 0.0 | A and B reach island on fumes, refuel |
| 0.5000 | 0.5000 | 1.0000 | 1.0000 | 180.0 | 0.0 | 0.0 | A and B depart counter-clockwise |
| 0.6875 | 0.1250 | 0.6250 | 0.6250 | 247.5 | 292.5 | 292.5 | C transfers 1/4 tank to B |
| 0.6875 | 0.1250 | 0.8750 | 0.3750 | 247.5 | 292.5 | 292.5 | C turns back |
| 0.7500 | 0.0000 | 0.7500 | 0.2500 | 270.0 | 270.0 | 315.0 | B refuels A with 3/8 tank |
| 0.7500 | 0.3750 | 0.3750 | 0.2500 | 270.0 | 270.0 | 315.0 | B turns back |
| 0.8750 | 0.1250 | 0.1250 | 0.0000 | 315.0 | 315.0 | 360.0 | C refuels |
| 0.8750 | 0.1250 | 0.1250 | 1.0000 | 315.0 | 315.0 | 360.0 | C turns back |
| 0.9375 | 0.0000 | 0.0000 | 0.8750 | 337.5 | 337.5 | 337.5 | C refuels A and B with 7/24 tank each |
| 0.9375 | 0.2917 | 0.2917 | 0.2917 | 337.5 | 337.5 | 337.5 | C turns back |
| 1.0000 | 0.1667 | 0.1667 | 0.1667 | 360.0 | 360.0 | 360.0 | All arrive with 1/6 of a tank |
Notes:
* It was not required to transfer this much fuel. As long as all planes had at least 1/8 of a tank to get back all would have enough to make it back to the island. I chose 7/24 so that each plane would have the same amount of emergency fuel, in the interests of safety.
I found this problem in the book My Best Mathematical and Logic Puzzles by Martin Gardner, which I highly recommend. It is problem 19.
Michael Shackleford, Dec. 3, 2017
| | | 230. | Five coins problem
| | | Two players, Sam and Dan, each have five coins. Both must choose to place one to five coins in his hand. At the same time, each must reveal the number of coins played. If both choose the same number of coins, then Sam will win collect all coins played. If both choose different numbers of coins, then Dan will collect all coins played. Assuming both players are prefect logicians, what is the optimal strategy for Dan?
Answer Problem 230 Answer
Dan should pick x coins with probability pr(x), as follows:
pr(1) = 77/548
pr(2) = 107/548
pr(3) = 117/548
pr(4) = 122/548
pr(5) = 125/548
Michael Shackleford, Jan. 15, 2018
Problem 230 Solution
It stands to reason that Sam's expected win should be the same regardless of whatever he picks.
Let p1 = Probability Dan picks 1 coin
Let p2 = Probability Dan picks 2 coins
Let p3 = Probability Dan picks 3 coins
Let p4 = Probability Dan picks 4 coins
Let p5 = Probability Dan picks 5 coins
If Sam picks one coin, then Sam's expected value is p1×2 - p2×3 - p3×4 - p4×5 - p5×6
If Sam picks two coins, then Sam's expected value is p1×-3 + p2×4 - p3×5 - p4×6 - p5×7
If Sam picks three coins, then Sam's expected value is p1×-4 - p2×5 + p3×6 - p4×7 - p5×8
If Sam picks four coins, then Sam's expected value is p1×-5 - p2×6 - p3×7 + p4×8 - p5×9
If Sam picks five coins, then Sam's expected value is p1×-6 - p2×7 - p3×8 - p4×9 + p5×10
Setting the expected value of Sam picking one to Sam picking two:
p1×2 - p2×3 - p3×4 - p4×5 - p5×6 = p1×-3 + p2×4 - p3×5 - p4×6 - p5×7
p1×5 - p2×7 + p3×1 + p4×1 + p5×1
Setting the expected value of Sam picking one to Sam picking three:
p1×2 - p2×3 - p3×4 - p4×5 - p5×6 = p1×-4 - p2×5 + p3×6 - p4×7 - p5×8
p1×6 + p2×2 - p3×10 + p4×2 + p5×2
Setting the expected value of Sam picking one to Sam picking four:
p1×2 - p2×3 - p3×4 - p4×5 - p5×6 = p1×-5 - p2×6 - p3×7 + p4×8 - p5×9
p1×7 + p2×3 + p3×3 - p4×13 + p5×3
Setting the expected value of Sam picking one to Sam picking five:
p1×2 - p2×3 - p3×4 - p4×5 - p5×6 = p1×-6 - p2×7 - p3×8 - p4×9 + p5×10
p1×8 + p2×4 + p3×4 + p4×4 - p5×16
It goes without saying that p1 + p2 + p3 + p4 + p5 = 1
Now we have five equations and five unknowns. Here is our matrix for these equations:
| 5 | -7 | 1 | 1 | 1 | 0 |
| 6 | 2 | -10 | 2 | 2 | 0 |
| 7 | 3 | 3 | -13 | 3 | 0 |
| 8 | 4 | 4 | 4 | -16 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
A little matrix algebra gives us:
pr(1) = 77/548
pr(2) = 107/548
pr(3) = 117/548
pr(4) = 122/548
pr(5) = 125/548
Michael Shackleford, Jan. 15, 2018
| | | 231. | Semi-circle inscribed in a quarter-circle problem
| | | A semi-circle is inscribed in a quarter-circle, as shown in this diagram.
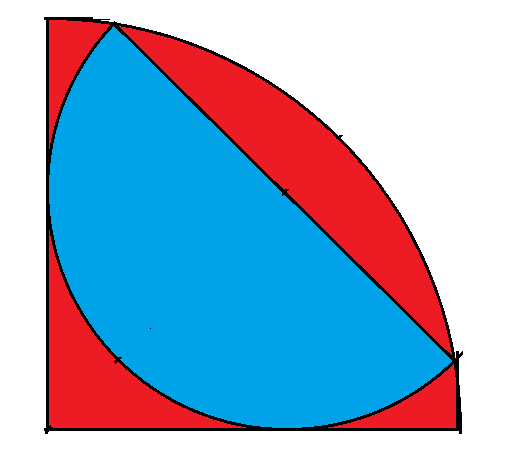
What is the ratio of the area of the semi-circle to the quarter-circle?
Answer
Problem 231 Answer
The answer is 2/3.
Michael Shackleford
Solution | | | 232. | Which is more e^pi or pi^e?
| | | Which is more πe or eπ?
Answer
Problem 232 Answer
eπ is greater.
Michael Shackleford
Solution | | | 233. | Rook in the corner
| | | A rook is placed at the corner of a chess board. Draw a path that goes through every square exactly once and end at the opposite corner, or prove it is impossible.
Answer
Problem 233 Answer
It is impossible. See the solution for why.
Michael Shackleford
Solution
Problem 233 Solution
Since the rook can go vertical and horizontal only, it must alternate going through black and white squares. There are 8*8=64 total squares on the chess board. After an odd number of moves, it must be on an opposite color square as that it started on. After an even number, the same color. There are 64 squares on the chess board, meaning 63 moves movements from one square to the other. Since 63 is odd, it must end up on a square of the opposite color. Opposite corners will be the same color, thus it is impossible.
Michael Shackleford
| | | 234. | Solve (x^2-15x+55)^(x^2-9x+20)=1
| | | Find all solutions of (x2 - 15x + 55)(x2 -9x + 20).
Answer
Problem 234 Answer
There are six solutions. Scroll down 100 lines for them.
The solutions are 4, 5, 6, 7, 8, and 9.
Michael Shackleford
Solution
Problem 234 Solution
The question is to solve for all values of x where (x2 - 15x + 55)(x2 -9x + 20) = 1.
Let's take the log of both sides...
(x2 -9x + 20) ln(x2 - 15x + 55) = 0
One way this can be true is if x2 -9x + 20 = 0
Let's factor the left side.
(x-4) × (x-5) = 0
So, the equation seems to be true for x = 4 and x = 5. Let's plug them into the original equation, to make sure we don't run into a 0^0 problem.
Let's do x=4 first:
(42 - 15×4 + 55)(42 -9×4 + 20) = 11^0 = 1, so that's good.
Let's do x=5 next:
(52 - 15×5 + 55)(52 -9×5 + 20) = 5^0 = 1, so that's good too.
But are there other values of x that work?
We also know (or at least we should know) that ln(1) = 0.
This will be true if x2 - 15x + 55 = 1.
Subtract 1 from both sides:
x2 - 15x + 54 = 0.
Factor that:
(x-9) × (x-6) = 0
So, the equation will also be true for x = 6 and x = 9. But any other values of x?
Recall that (-1)x = 1, if x is any positive integer.
The original equation will be true if x2 - 15x + 55 = -1 and x2 -9x + 20 is a positive integer.
First, let's try to find values where x2 - 15x + 55 = -1. Adding one to each side:
x2 - 15x + 56 = 0
Factoring:
(x-7) × (x-8) = 0
We get x=7 and x=8. Let's plug those into x2 -9x + 20, to make sure it is positive.
72 -9*7 + 20 = 6, so x=7 is good.
82 -9*8 + 20 = 12, so x=8 is good.
So, there are six values for x that work: 4, 5, 6, 7, 8, and 9.
This problem was inspired by a similar one by Presh Talwalker, which he goes over in the video Most Computers Can't Solve This, But You Can.
Michael Shackleford
| | | 235. | Hanging rope problem
| | | A 100-meter rope is suspended from the top of two 50-meter poles. The lowest point of the rope is 10 meters from the ground. How far apart are the poles?
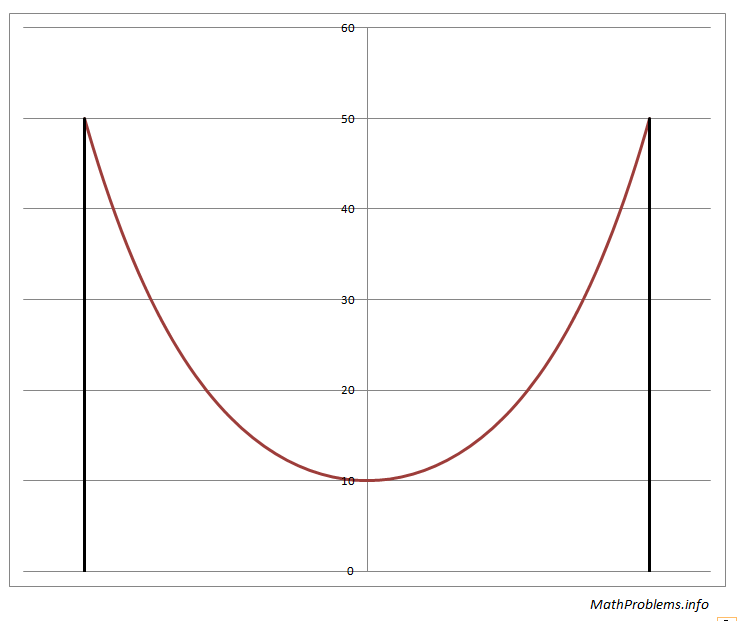
For some helpful equations, please see these hints.
Answer
Problem 235 Answer
The answer is 45×ln(3) = 49.4376 meters.
Michael Shackleford
Solution | | | 236. | Three circles problem #3
| | | What is the distance from A to B in this diagram: 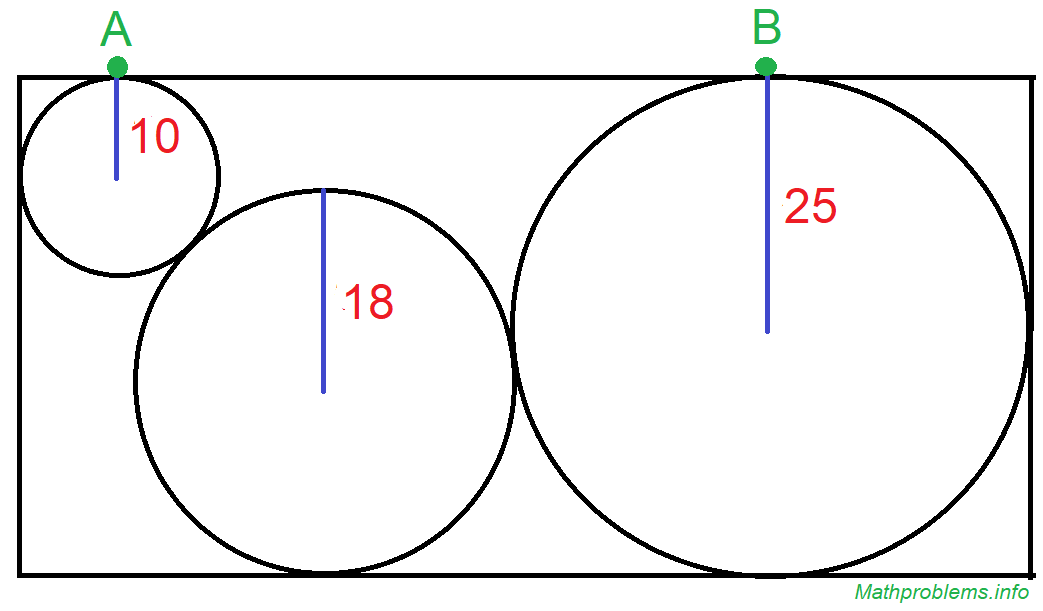 . .
Answer
Problem 236 Answer
The answer is 30*sqrt(2) + 10*sqrt(3) = 59.7469.
Michael Shackleford
Solution | | | 237. | Three ants problem
| | | Three ants go around the circumference of a circle, each at his own contant rate and in the same direction. It takes ant A three minutes to make a revolution, ant B five minutes, and ant C seven minutes. They all start out at random points. A point is picked at random on the circumference. What is the probability each ant reaches that point first?
Answer
Problem 237 Answer
Problem 237 Answer
Here are the probabilities each ant arrives first:
- Ant A: 20/35 = 57.14%
- Ant B: 9/35 = 25.71%
- Ant C: 6/35 = 17.14%
Michael Shackleford
Solution | | | 238. | Two boards and a moat
| | | A castle is on a square island, surrounded by a moat 25 feet wide. You have two 24 foot boards, but no nails or any other way to attach them to each other. How can you place the boards to get to the island? For extra credit, how is the shortest length the two boards can be and still reach the island?

Answer
Problem 238 Answer
Place one board across a corner of the moat and the other from the center of that board to the corner of the island, making a T shape with the boards.
The shortest length the boards can be is 50*20.5/3 =~ 23.5702 feet.
Michael Shackleford
Solution
Problem 238 Solution
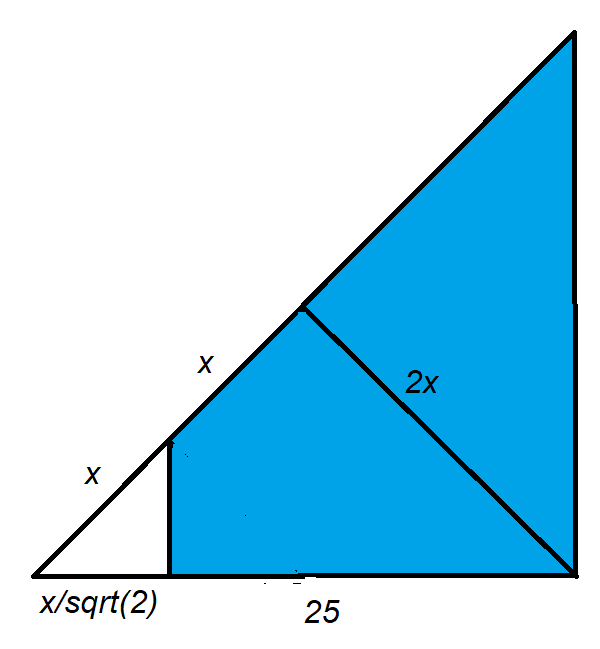
- Let the ladder be the length 2x.
- From the diagram above, we can set up the equation: (2x)2 + (2x)2 = (x/20.5 + 25)2
- 8x2 = (x*20.5/2 + 25)2
- 8x2 = x2/2 + 25x*20.5 + 1250
- 15x2 - 50x*sqrt(2) - 1250 = 0
- x = [50*20.5 +/- (5000 + 75000)0.5]/30
- x = 25*20.5/3
- The whole ladder is length 2x, so the answer is 50*20.5/3 =~ 23.5702 feet.
Michael Shackleford
| | | 239. | 3 hot dog vendors and a beach
| | | There is a beach one mile long. It is a nice day so a big crowd of people are expected, who will be equally distributed along the beach. When anyone gets hungry, he heads to the nearest hot dog stand. Three logicians operate hot dog carts and arrive to the beach one at a time before the crowds arrive. A is first, then B, and finally C. All three will locate their stand with the goal of maximizing sales for the day. Once a spot is picked, the vendor must stay there all day. The vendors don't trust each other, so collusion is out. B will note the location of A and choose his location accordingly. C will note the locations of A and B and pick his location accordingly. Where should A set up his stand? How much of the beach will each vendor get, assuming all follow optimal strategy. You may assume that if a vendor is indifferent between multiple locations, then he will pick randomly.
Answer
Problem 239 Answer
Problem 239 Answer
The first should go either a smidge to the left of the point 1/4 from the left end of the beach and a smidge to the right of the point 3/4 from the right end.
The second vendor will pick the spot from A's two choices that A didn't pick.
The third vendor will go in the middle.
This will give A and B 3/8 of the beach each, and C 1/4.
Michael Shackleford
Solution
Problem 239 Solution
Problem 239 Solution
It stands to reason that A and B will want C to go in the middle, least he be the closest to an edge and cut them off from that section of the beach. How far can they extend away from an edge and still keep C in the middle?
Let's call x the distance from either edge that would put C indifferent between going right next to A and B but closer to an edge and the middle.
At x, assuming C goes in the middle, A will get x + (0.5 - x)/2 = x/2 + 1/4 of the beach. Same with B. C will bet (1-2x)/2 = 1/2 - x of the beach.
If C located right next to A or B, but closer to an edge, he would get territory of length x. So, we want to equate x and (1/2 - x) to find that indifference point for C.
x = 1/2 - x
2x = 1/2
x = 1/4
To make sure C isn't indifferent, and barely prefers the middle, A and B should go just a smidge closer to the edges than the 1/4 and 3/4 points. This will give A and B a smidge less then 3/8 of the beach each and C a smidge more than 1/4.
Michael Shackleford
| | | 240. | 4 hot dog vendors and a beach
| | | Same problem as 239, except four vendors.
Answer
Problem 240 Answer
Problem 240 Answer
A will set is stand a smidge less than 1/6 of a mile from either end.
B will do the same as A, but at the opposite end.
C will set his stand exactly in the middle of the beach.
D will be indifferent between placing his stand between either (1) A and C and (2) B and C.
Michael Shackleford
Solution
Problem 240 Solution
Problem 240 Solution
A will want to pick a spot close to either edge, maximizing his space without giving another vendor the incentive to put his stand right next to his on the side close to the edge. It is good to be close to an edge, because you get every customer between you and that edge. Let's just say he picks the left side of the beach.
B will want to do the same, but on the right side.
C will pick a spot in the middle, putting D to an indifference point which side of C to go on.
D will arbitrarily pick a spot between A and C or B and C.
The question is how far from the edge should A and B pick?
We want D to pick on either side of C. Let's ask the question at what point would D be indifferent between going just to the left of A, between A and C, and between B and C.
If A sets his stand at point x, then D would get x miles just to the left of A or (1/2-x)/2 by going between A and C or B and C. Let's set these two equations equal to each other and solve, to find the indifference point for x.
x = (0.5-x)/2
2x = 0.5 - x
3x = 0.5
x = 1/6
However, we don't want D to be indifferent, we want him to pick a spot on either side of C. So, we pick a spot a smidge to the left of 1/6, to get D to go next to C.
Same logic for B -- a smidge to the right of 5/6.
C will want to make D indifferent to going on either side of him, which is obviously 1/2.
D will then arbitrarily picks between 1/3 and 2/3.
A will then get 1/4 if D picks 3/8 and 1/3 if he picks 5/8. The average of those two is 7/24.
B is in the same situation as A, so 7/24 on average to him too.
Let's say D flips a coin and goes in the 1/3 spot. Then C will get everything from the 5/12 to the 2/3 point, which is 1/4 mile.
With D and the 1/3 spot, he will everything from the 1/4 to the 5/12 points, which is 1/6 mile.
Michael Shackleford
| | | 241. | 10 playing cards and a dark room
| | | In a dark room there is a deck of cards with 10 face up and the rest face down. Your task is to divide the total deck into two piles so that the same number of face up cards is in each pile. Remember, it is dark so you can't see the cards. How do you do it?
Answer
Problem 241 Answer
Problem 241 Answer
Place ten cards in one pile with the other 42 cards in the other. Then, flip over the ten-card pile.
Michael Shackleford
Solution
Problem 241 Solution
Problem 241 Solution
Place ten cards in one pile with the other 42 cards in the other. Let's say the 10-card pile has x face up cards and 10-x face down cards. The 42-card pile will have 10-x face up cards.
Then flip over the 10-card pile. It will now have 10-x face up cards, the same as the 42-card pile.
Michael Shackleford
| | | 242. | Maximum volume of cone
| | | You are in charge of making cone-shaped paper cups. Your goal is to maximize the ratio of volume to surface area. What is the maximum that ratio can be? Assume the length from the tip of the cup to any point on the edge is 1.
Answer
Problem 242 Answer
Problem 242 Answer
The answer is 1/6.
Michael Shackleford
Solution
Problem 241 Solution
Problem 242 Solution
Please see my problem 242 solution (PDF -- 97K)
Michael Shackleford
| | | 243. | Secret Santa
| | | Your office of 100 workers does a Secret Santa gift exchange. This where you write down everybody's name on individual pieces of paper, put them in a hat, and everybody draws a name at random to give a gift to.
The question is, how many closed loops will there be, on average? For example of a closed loop, Gordon gives to Don, who gives to Jon, who gives to Nathan, who gives to Gordon. Or drawing your own name.
Answer
Problem 243 Answer
Problem 243 Answer
The answer is 1/1 + 1/2 + 1/3 + ... + 1/100 =~ 5.187377518.
Michael Shackleford
Solution
Problem 243 Solution
Problem 243 Solution
Consider everybody choosing one at a time.
Let f(n) equal the average number of closed loops with n people.
When the first person picks, there is a 1/100 chance he picks himself and 99/100 he doesn't. In other words, there is a 1/100 chance he closes a loop and 99/100 he doesn't. Either way, it reduces the problem to one of 99 people. In other words, f(100) = (1/100) + f(99).
When the second person goes, he will have a 1/99 chance of closing a loop and 98/99 he doesn't. Whatever happens with the first person, there can be only one name left that started an unclosed loop. Thus, f(99) = 1/99 + f(98). Or, f(100) = (1/100) + (1/99) + f(98).
This process keeps repeating until there is just one person left, who will close the last loop, since the person who started it must be the only name left.
Thus the answer is 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518.
An estimate for any sufficiently large n is ln(n).
Michael Shackleford
| | | 244. | Connecting four points on a square
| | | There is a square-shaped state with a town at each corner. Your goal is to build a network of roads linking the four towns together, minimizing the total length of the roads. For example, this could be done with an X shape, but there is a better way. Assuming the side of the square is 200 kilometers, what is the minimum length of the roads? (Hint on the shape of the road network.)
Answer
Problem 244 Answer
Problem 244 Answer
Here is the general shape of the road network:
The minimum road distance is 200 * (3*sqrt(3)/3 + 1) =~ = 546.4102 kilometers.
Michael Shackleford
Solution
Problem 244 Solution
Problem 244 Solution
Here is the general shape of the road network:
The total length of the roads will be 4x+z.
We're told the length of the side of the state is 200, However, let's assume a side length of 1, to be more elegant, and multiply by 200 at the end.
If a side of the square is 1, then 2y+z = 1.
Rearranging, z = 1 - 2y.
So, the total distance can be expressed as 4x + 1 - 2y.
From the Pythagorean formula, 0.5^2 + y^2 = x^2.
Rearranging, y^2 = x^2 - 0.25.
y = (x^2 - 0.25)^0.5
To put the total distance as a function of just x:
f(x) = 4x + 1 - 2*(x^2 - 0.25)^0.5.
Next, set the derivative to equal zero, to find the value of x that maximizes f(x).
f'(x) = 4 - 2*0.5*2x*(x^2 - 0.25)^-0.5 = 0.
2*0.5*2x*(x^2 - 0.25)^-0.5 = 4
x*(x^2 - 0.25)^-0.5 = 2
x = 2*(x^2 - 0.25)^0.5
x^2 = 4 * (x^2 -0.25)
3x^2 = 1
x^2 = 1/3
x = sqrt(3)/3
Our total road length, based on a side of 1, is:
4*sqrt(3)/3 + 1 - 2*(1/3 - 1/4)^0.5 =
4*sqrt(3)/3 + 2*(1/12)^0.5 =
4*sqrt(3)/3 + 1 + 2*0.5*sqr(3)/3 =
3*sqrt(3)/3 + 1 =~ 2.7321
So, for a side of length 200 kilometers, the answer is 200 * (3*sqrt(3)/3 + 1) =~ = 546.4102 kilometers.
Michael Shackleford
| | | 245. | Leaping frog
| | | There is a frog at the bottom of 20 steps. With each jump, the frog can jump up one or two steps. The frog eventually lands on exactly on the 20th step. What is the number of possible permutations of jumps, in order, the frog can take. For example, 1-1-1-1-1-2-2-2-2-2-1-1-1-1-1.
Answer
Problem 245 Answer
Problem 245 Answer
The answer is 10,946.
Michael Shackleford
Solution
Problem 245 Solution
Problem 245 Solution
Let a jump of one step be a "small jump" and a jump of two steps be a "big jump."
- There is only one way to get to the first step, with a single small jump.
- There are two ways to get to the second step, either two small jumps or one big jump.
- There are two ways to arrive at the third step, either with a big jump from step 1 or a small jump from step 2. There is one way to arrive at step 1 and two ways to arrive at step 2. Thus, the number of ways to get to step 3 is 1 + 2 = 3.
- There are two ways to arrive at the step 4, either with a big jump from step 2 or a small jump from step 3. There are 2 ways to arrive at step 2 and 3 ways to arrive at step 3. Thus, the number of ways to get to step 4 is 2 + 3 = 5.
- There are two ways to arrive at the step 5, either with a big jump from step 3 or a small jump from step 4. There are 3 ways to arrive at step 3 and 5 ways to arrive at step 4. Thus, the number of ways to get to step 4 is 3 + 5 = 8.
- Keep following this logic and you will find that there are 10,946 ways to arrive at the 20th step.
Here is the full Fibbonachi sequence, up to 20:
- 1
- 2
- 3
- 5
- 8
- 13
- 21
- 34
- 55
- 89
- 144
- 233
- 377
- 610
- 987
- 1597
- 2584
- 4181
- 6765
- 10946
Michael Shackleford
| | | 246. | Common birthday for three or more people
| | | In an office of 200 people, what is the probability any five or more people will share a common birthday?
Answer
Problem 246 Answer
Problem 246 Answer
The answer is 0.0880680413.
Michael Shackleford
Solution
Problem 246 Solution
Problem 246 Solution
- First a note about terminology, let C(x,y) equal the number of ways to choose y items out of x. The formula is x!/(y! × (x-y)!). For example, the number of way to choose five cards out of 52 is C(52,5) = 52!/(5! × 47!) = 2,598,960.
- Rather than keep using the word "birthday," let's say each person will get one "day."
- Next, let's consider the case of five people sharing a common birthday. The logic will work for any number of people sharing a common birthday.
- To make a specific example, consider the probability that in an office of 200 people there will be at least one day of the year shared by five or more people.
- To find that answer, first find the probability that in 200 people nobody day will be shared by five or more people. Subtracting that answer from 1 will give us the probability of a common birthday to five or more people.
- There are 365200 possible sequences.
- To find the number of sequences where there is no day celebrated by five or more people, consider all the ways to clump the 200 people into days shared by 4 people, shared by 3, shared by 2, and shared by 1.
- Let a = the number of days shared by 4 people. This number can be 0 to 50.
- Let b = the number of days shared by 3 people. This number can be 0 to int((200-4a)/3).
- Let c = the number of days shared by 2 people. This number can be 0 to int((200-4a-3b)/2).
- Let d = the number of days occupided by just one person. This number must be 200-4a-3b-2c.
- The number of ways you can assign specific days to each of these days with at least one birthday is C(365,a)×C(365-a,b)×C(365-a-b,c)×combin(365-a-b-c,d). Let's call that number p.
- The number of ways to order the 200 birthdays is 200!. Multiply that by p.
- If we stopped here, p would be too big. Why? Let's say two people share May 23. Let's go onto say that if you lined up all 200 people they took spots 81 and 144. It wouldn't make any difference which May 23 person got 81 and who got 144. The sequence of birthdays would still look the same.
- Likewise, we would divide by 3!=6 for each group of 3 people, and 4!=24 for each group of 4 people.
- To adjust for the c groups of 2 people, divide p by 2c.
- To adjust for the b groups of 3 people, divide p by 6b.
- To adjust for the a groups of 4 people, divide p by 24a.
- That will give us the correct value of p, the number of sequences of birthdays where no day is shared by 5 or more people.
Thus, the probability of no common birthday is C(365,a)×C(365-a,b)×C(365-a-b,c)×combin(365-a-b-c,d)/(2c × 6b × 24a)/365200, for all possible combinations of a, b, c, and d. This works out to 0.9119319587.
So, the probability of at least one day common to five or more people is 1 - 0.9119319587 = 0.0880680413.
As a practical note, there is no easy way to get at this number without a computer. Here is my code that shows how to calculate the probability of no common birthday, where p is the number of 200:
tot_pr=0;
for (a=0; a<=(int)p/4; a++)
{
for (b=0; b<=(int)((p-4×a)/3); b++)
{
for (c=0; c<=(int)((p-4×a-3×b)/2); c++)
{
d=p-4×a-3×b-2×c;
pr=combin(365,a);
pr×=combin(365-a,b);
pr×=combin(365-a-b,c);
pr×=combin(365-a-b-c,d);
pr/=(double)power(24,a);
pr/=(double)power(6,b);
pr/=(double)power(2,c);
for (i=1; i<=p; i++)
{
pr×=(double)i;
pr/=365.0;
}
tot_pr+=pr;
}
}
}
printf("%i\t%12.10f\n",p,tot_pr);
cerr << p <<"\t" << tot_pr<< "\n";
Michael Shackleford
| | | 247. | Semicircle in a rectangle
| | | What is the area in green?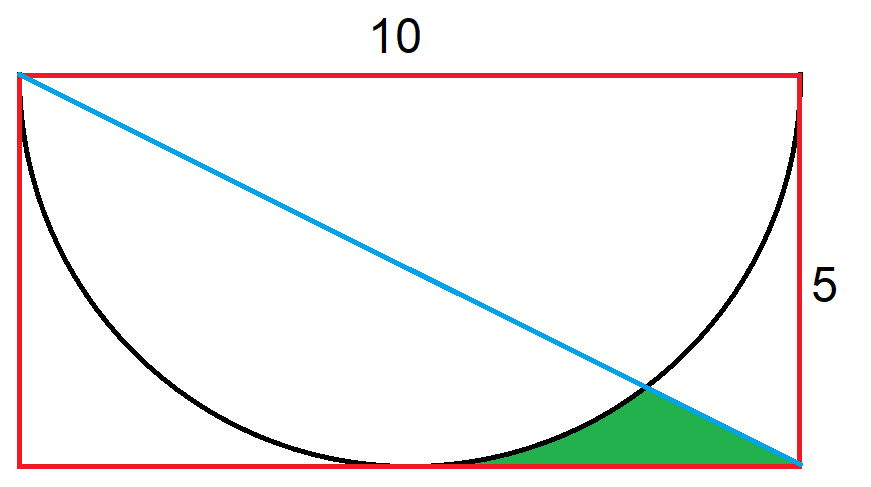 . .
Answer
Problem 247 Answer
Problem 247 Answer
The answer is 10 - 12.5×cos-1(4/5) =~ 1.95624.
Michael Shackleford
Solution
Problem 247 Solution
Problem 247 Solution
Please see my problem 247 solution (PDF).
Michael Shackleford — May 6, 2019
| | | 248. | Sphere in a tetrahedron | | | Consider a sphere inscribed in a tetrahedron, where each side of the tetrahedron is an equilateral triangle with sides of length 1. What is the ratio of the area of the sphere to the tetrahedron?
Answer
Problem 248 Answer
Problem 248 Answer
The answer is approximately 0.302299894.
Michael Shackleford
Solution
Problem 248 Solution
Problem 248 Solution
- Let's start by finding the height of any of the sides. Consider the right triangle formed by that height, the side of a triangle, and half of another side. Let the height be x. So we have:
1^2 = 0.5^2 + x^2
x^2 = 0.75
x = sqrt(0.75) =~ 0.866025404
- Next, let's find the distance from the center of that triangular side to the middle of any edge. Call that distance x. Consider the right triangle with legs x and 0.5. The hypotenuse equals the height less x. Let's call the height h. So, we have a right triangle with sides of 0.5, x, and hypotenuse h-x. Using the Pythagorean Theorem, we can solve for x as (h^2-0.25)/(2*h). We know h from the last step, so the distance from the center of that triangular side to the middle of any edge =~ 0.288675135.
- Next, let's find the distance from the center of the triangle to a corner. Consider the right triangle formed by the corner of the side of the equilateral triangular side of the tetrahedron, center of that triangle, and the middle of any side of that equilateral triangular. We know the two legs of that right triangle are 0.5 and 0.288675135, so using the Pythagorean Theorem we can find the distance from the corner of the triangle to the center is approximately 0.577350269.
- Next, let's find the height of the tetrahedron. Imagine the tetrahedron laying flat. Consider the right triangle formed by a corner of the tetrahedron on the base, center of the base, and top of the tetrahedron. We know the hyppotenuse of that triangle is 1 and one leg is the distance from the corner of the triangle to the center, which we solved for in the last step. Using the Pythagorean Theorem yet again, we can find the height of the tetrahedron is 0.816496581.
- Next, let's find the distance from the center of any side of the tetrahedron to the center of the tetrahedron. Here is a trick to easily finding that. Continue to think of the tetrahedron with a side flat on the ground. The height from the ground of three of the corners is 0. The height of the fourth corner is the height of the tetrahedron, which we just solved for.
- The height of the center will be the average of the height of each corner. In other words the height is (0+0+0+0.816496581)/4 = 0.816496581/4 = 0.204124145. This is the radius of the sphere inside the tetrahedron.
- Next, let's find the area of one of the sides of the tetrahedron. The area is (1/2)*side*height = (1/2)*1*0.816496581 = 0.433012702.
- Next, let's find the area of the tetrahedron. The formula is (1/3)*base*height = (1/3)*0.433012702*0.816496581 = 0.117851130.
- Next, let's find the volume of the sphere. The formula for that is (4/3)*pi*r^3 = (4/3)*pi*0.204124145^3 = 0.035626384.
- Finally, our answre is the area of the sphere divided by the area of the tetrahedron = 0.035626384/0.117851130 = 0.302299894.
Michael Shackleford — May 6, 2019
| | | 9. | Chicken McNugget problem
|  | | At McDonalds you can order Chicken McNuggets in boxes of 6, 9, and 20. What is the largest number such that you can not order any combination of the above to achieve exactly the number you want?  Answer
Answer
Problem 9 Answer
Problem 9 Answer
The answer is 43.
Michael Shackleford, A.S.A.
Solution
For any desired number if it is divisible
by 3 it can easily be made with 6 and 9 packs,
except if the number is 3 itself. If you can't
use all six packs then use one 9 pack and you
can do the rest with six packs.
If the number is not divisible by 3 then
use one 20 pack. If the remaining number is
divisible by 3 then use the above method for
the rest.
If the number still isn't divisible by 3 use
a second 20 pack. The remainder must
be divisible by 3, in which case use the 6 and 9
packs as above.
The largest impossible number would be such that
you would have to subtract 20 twice to get a
remainder divisible by 3. However, you can't
make 3 itself with 6 and 9 packs. So the
largest impossible number is 2*20+3=43.
Michael Shackleford, A.S.A.
|
|