Partial differential equations required.
Water flows into a tank at a rate of 1 gallon per second. Water leaves
the tank at a rate of 1 gallon per second for each 100 gallons in the
tank. The tank is initially empty. How long will it take for the
tank to fill with 50 gallons of water?
(Answer),
(Solution).
Probability and algebra requied.
A drunk is on one point of an n-gon, such that n is an even number. The drunk moves along
the perimeter of the n-gon. Each steps takes him to an adjacent point, and every step is
chosen at random. What is the expected number of steps before he arrives at the point
directly opposite of his starting point (as a function of n)?
(Answer),
(Solution).
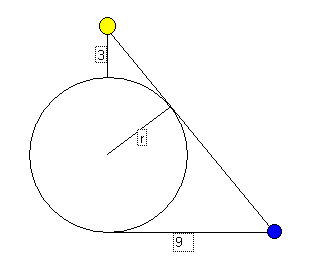
There exists a city surrounded by a circular wall. The wall has two gates, one on the north end and one on the south end. A yellow house exists 3 miles north of the north gate. A blue house exists 9 miles east of the south gate. The yellow and blue houses can barely see other around the side of the wall. What is the radius of the circle formed by the wall? You may visit the The MathServ Calculus Toolkit for help factoring polynomials. (Answer), (Solution).
Probability and infinite sums requied.
You are given an initial prize of one dollar. A coin will be tossed indefinitely until a
tails occurs. Every time a heads is tossed your prize will be doubled. When a tails is
tossed you walk away with whatever your prize has grown to. For example if you toss three
heads and then tails you would get $1*2*2*2=$8 dollars. What is the expected return of
this game?
(Answer),
(Solution).
Integral calculus and trigonometry required.
What is the ratio of the surface area of the state of Colorado to
the surface area of the earth? You may assume that
the lower and upper lines of latitude are 37 degrees and 41 degrees, and that
the east and west lines of longitude are 102 and 109 degrees (the latitude lines
I believe are exactly right and the longitude lines are very close and both
appear to be off by about the same amount in the same direction). You may also
assume the earth is perfectly spherical (which it isn't).
(Answer),
(Solution).
Probability and infinite sums requied.
Assuming you flipped a coin until over and over, keeping track of the number of
both heads and tails flipped, what is the expected number of flips before the
two totals were equal?
(Answer),
(Solution).
Geometry required.
What is the height of a pentagon with side length of 1? Answer
many not be expressed in trigonometric functions.
(Answer),
(Solution).
Geometry required.
What is the volume of a dodecahedron with side (of pentagon)
equal to 1? Hint: you may wish to solve problem problem 123 first.
(Answer),
(Solution).
Interest theory requied.
This situation actually happened to me at Toyota
of Garden Grove, although the numbers were changed for
the benefit of simplicity: You are about to pay
$10,000 cash for a new car. The finance manager, wanting to
loan you money, asks you what interest rate you could earn on
that money if you didn't spend it. You answer 6%, compounded
monthly. The finance manager then says that he will give you
a loan at 7.5% interest, compounded monthly, with a
five year term. He then shows you on his computer that
if you invested the $10,000 on your own you would earn $3,488.50
in interest in five years. Then he shows you that your payments on the
car would be $200.38 a month, making total interest paid
on the car $2,022.77. You do the math on your own and you
realize it is correct. He then argues that you would
come out ahead by taking out a loan since you would make more
in interest than you would pay. Is this argument valid?
(Answer),
(Solution).
Probability required.
The world series consists of up to seven games, the first team to win
four wins the series. Team A will play in their home field games 1, 2,
and 5, 6, and 7 if necessary. Games 3, 4, and 5 (if necessary) will be
played at team B's home field. Assuming each time has a 50% chance
of winning every game, which team will is more likely have have the home field
advantage the majority of the time? For extra credit what is the expected number
of games played in each home field?
(Answer),
(Solution).
Geometry and derivative calculus required.
You have a circular piece of paper with radius 1 and wish to form a cone shaped cup. You may
cut out any wedge you like from the paper, call the angle of the wedge x. The
point of the wedge must be at the center of the circle. After
cutting out the wedge you then attach the two straight edges remaining to form a
cone. Assuming the paper cone can hold water, what should x be to maximize the water
holding capacity of the cone?
(Answer),
(Solution).
A woman is chosen at random among all women that have two children. She is asked
do you have at least one boy, and she answers 'yes.' What is the probability her
other child is a boy? Assume every pregnancy has a 50/50 chance to be a boy or a
girl.
(Answer),
(Solution).
Derivative calculus required.
Your job allows you to work any number of hours per week you desire. Your take
home pay is proportional to the number of hours worked (no overtime). After
subtracing time for sleeping and routine daily tasks you have 80 hours per
week left for work and pleasure. You wish to maximize your income
multiplied by the amount of pleasure time you have to enjoy it. How many hours
per week should you work?
(Answer),
(Solution).
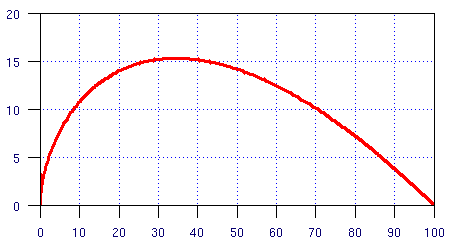
Partial differential equations required.
A bird is flying towards its nest which is 100 feet away due east. Without
considering the wind the bird can fly at a speed of 5 feet per second.
There is a north blowing wind, however, at a speed of 2 feet per second.
At all times the bird is flying in a direction such that he is directly
facing the nest. The bird is not tacking into the wind as a boat would
do but is continuously being blown off course and trying to set a new
course. The graph above shows the path of the bird. How long does it
take for the bird to reach the nest?
(Answer),
(Solution).
Probability required.
A baby is added to a hospital nursery. Before the baby was added there
were two boys in the nursery and an uncounted number of girls. After the
new baby is added a baby is selected at random among all the babys. The
selected baby is a boy. What is the probability that the added baby was
a girl?
(Answer),
(Solution).
No math required but spacial relations helpful.
Given an 2n by 2n chessboard, with one
corner removed, show that you can cover it completely without
overlapping or going off the board using only triominoes of this shape:
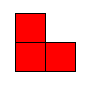
Rotations are allowed.
(Answer & Solution).
Simple math required.
How many subsquares can you form on chessboard with n*n unit
squares? Subsquares must be an integer squared.
(Answer),
(Solution).
Algebra required.
Show that any prime number other than 2 can be expressed as the difference
of two squares, where each square is an integer squared.
(Answer).
Computer helpful.
Two players are each dealt a card face down. Each player may look at his own card. The highest
card wins. Cards are valued as in poker
with aces being low. The first player may either keep his card or switch with the second player.
The second player may keep his card, whether it be his original card or one that the first player
gave him after switching, or trade it with the next card on the deck, which is also face down.
The loser pays the winner $1 and if both cards are equal then no money exchanges hands. For the
sake of simplicity assume an infinite number of decks. Both players are infinitely logical. At
what point should the first player switch? At what point should the second player switch if the
first player doesn't switch? What is the expected gain of the first player?
(Answer),
(Solution).
