Problem 47 Solution

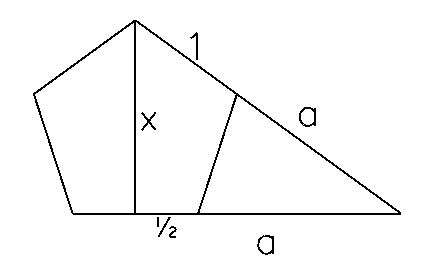
Let x be the height of the pentagon and a be the length of the extensions of the sides, as shown in the following diagram:

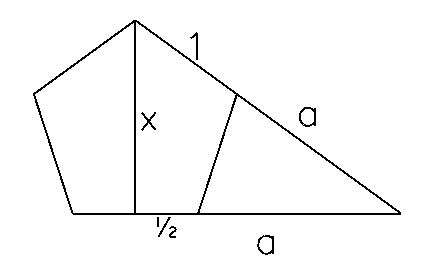
Using the Pythagorean formula we know x² + (a+1/2)² = (a+1)², or

(1) x² = a + 3/4.

Now consider the added two chords in the next diagram:

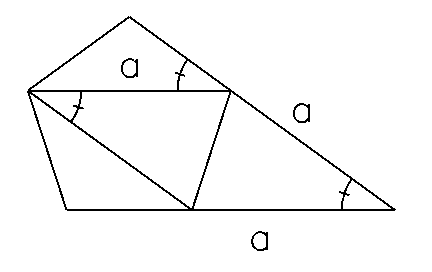
The isosceles triangle formed by these two chords and one side of the pentagon is congruent to the triangle formed by two extensions of length a and the same side of the pentagon.

Thus the distance between two non-adjacent corners of the pentagon is also a. Consider the chord going from either corner of the base to the top of the pentagon. We can use the Pythagorean formula, with this chord as the hypotenuse to obtain:

x² + (1/2)² = a².

Substituting for x² from above we can solve for a:

a + 3/4 = a² - (1/2)², or

a² - a - 1 = 0, or

a=(1+sqr(5))/2.

Now that we know a we can solve for x:

x² = ((1+sqr(5))/2)² - 1/4, or

x² = (5+2*sqr(5))/4, or

x = sqr(5+2*sqr(5))/2 =~ 1.538842

Old Solution

• sin(5x)=5*sin(x)-20*sin³(x)+16sin⁵(x).

• tan(x)=sin(x)/(1-sin²(x))^1/2.

• The interior angles of an n-gon are each 180*(n-2)/n.

With some simple trig we can express the height as 1/2*[1/sin(36) + 1/tan(36)].

From the formula in the hint we can express tan(36) as sin(36)/sqr(1-sin²(36)).

After a few simple steps we can express the height as (1) 1/2*[(1+sqr(1-sin²(36))/2*sin(36)].

Next lets work on expressing sin(36).

From the formula in the hint we know sin(180) = 16*sin⁵(36) - 20*sin³(36) + 5*sin(36)

= 16*sin⁴(36) - 20*sin²(36) + 5

= 16x⁴ - 20*x² + 5 (where x=sin(36)).

= 16y² - 20*y + 5 (where y=x²).

y = (5-sqr(5))/8.

x = sqr((5-sqr(5))/8) = sin(36).

Now put this expression for sin(36) into equation (1):

1/2 * [ (1+sqr(1-(5-sqr(5))/8)) / sqr((5-sqr(5))/8) ] =

1/2 * [ (1+sqr(3+sqr(5))/8)) / sqr((5-sqr(5))/8) ] =

1/2 * [ sqr(8/(5-sqr(5))) + sqr((3+sqr(5))/(5-sqr(5))) ] =

1/2 * [ (sqr(8) + sqr((3+sqr(5)))/(5-sqr(5))) ] =~ 1.5389