Logic required.
Of three men one man always tells the truth, one always tells lies,
and one answers yes or no randomly. Each man knows which man is who.
You may ask three yes/no question to determine who is who. If you
ask the same question to more than one person you must count it as question
used for each person whom you ask. What three questions
should you ask? (Answer).
Calculus required.
At dark is thrown at a dart board of radius 1. The dart can hit anywhere on the board
with equal probability. What is the mean distance between where the dart hits and
the center?
(Answer),
(Solution).
Simple math required..
Create the number 24 using only these numbers once each: 3, 3, 7, 7.
You may use only the following functions: +, -, *, /. This is not
a trick question, for example the answer does not involve a number system other
than base 10 and does not allow for decimal points.
(Answer).
Probability required, computer helpful.
In the Price is Right three players compete for one place in the
showcase showdown. Each player takes their turn spinning a wheel which
has an equal probability of stopping on every amount evenly divisible by .05
from .05 to 1.00 . If the player does not like their first spin they may
spin again, adding the second spin to their first, however if they go over
1.00 they are immediately disqualified. In the event of a tie the winner
is determined randomly with each player left having an equal probability of
winning. What is perfect strategy for all players in this game, assuming
that all other players also play by perfect strategy?
(Answer).
Calculus required.
There is a street of length 4. The street is initially empty. Cars then come
along to fill the street until there is no space left that is large enough to
park a car in. Every car is length 1. Drivers will choose a location to park
at random among all possible locations left. No consideration, whether good or
bad, is given to other cars. What is the expected number of cars that will be
able to park?
(Answer),
(Solution).
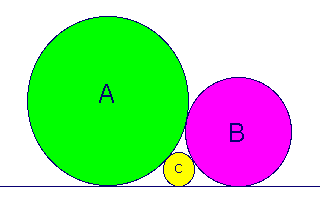
Geometry required. The three circles in the diagram above all are tangent to the line in the picture. The radius of circle A is a, of circle B is b, and of circle C is c. All three circles are tangent to each other. What is c as a function of a and b? (Answer), (Solution).
Simple math required.
Create the number 24 using only a 1, 3, 4, and 6. You may only
use +, -, /, and *. Parenthesis are allowed. For example if I asked
for 23 an answer would be ((6-1)*4)+3. This is not a trick question, for
example the answer does not involve a number system other
than base 10 and does not allow for decimal points.
(Answer).
Simple math required.
On a deserted island live five people and a monkey. One day everybody gathers
coconuts and puts them together in a community pile, to be divided the next day.
During the night one person decides to take his share himself. He divides the coconuts
into five equal piles, with one coconut left over. He gives the extra
coconut to the monkey, hides his pile, and puts the other four piles back into
a single pile. The other four islanders then do the same thing, one at a time,
each giving one coconut to the monkey to make the piles divide equally. What is
the smallest possible number of coconuts in the original pile?
(Answer),
(Solution).
Geometry required. The three colored circles in the diagram above
have radii of 1, 2, and 3, and each are tangent to the other two. A fourth interior
circle is tangent to all three colored circles. What is the radius of the
interior circle? For extra credit what is the radius of the exterior circle (not
pictured) that is tangent to the three colored circles?
(Answer),
(Solution).
It is speculated that the number 6 appears a disproportionately high number of
times and thus the digits are not distributed randomly. Test the hypothesis
that these digits form a random sample such that the outcome of 10,000 truly random
digits would pass the test 95% of the time.
(Answer),
(Solution).
Probability required.
You have two bags of m&m candy. One bag has 99 red candies and 1 blue candy. The other
bag has 99 blue candies and 1 red candy. You choose a bag at random, open it, and draw
just one candy from the bag. If the candy drawn is red what is the probability what is the
probability that it was drawn from the bag with 99 reds and 1 blue?
(Answer),
(Solution).
Geometry required.
There is a straight cable buried under a unit square field. You must dig one or more
ditches to
locate the buried cable. Where should you dig to guarantee finding the cable and to
minimize digging? For example you could dig an X shape for total ditch length of
2*sqr(2) but there is a better answer.
(Answer).
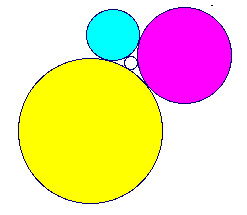
Statistics required.
In a drawer are two red socks and three blue socks. A sock is drawn at random from the
drawer, with replacement, one million times. What is the range, with the expected outcome as the
midpoint of the range, such that the probability is 95% that the number of red socks drawn falls within
this range?
(Answer),
(Solution).
Statistics required.
The following is a distribution of the first 10,000 digits of e:
0 974
1 989
2 1004
3 1008
4 982
5 992
6 1079
7 1008
8 996
9 968
Statistics required.
A gold mining company is testing locations for its next mine. From location A
eight samples were taken of units of gold per ton of ore. The results were
1.23, 1.42, 1.41, 1.62, 1.55, 1.51, 1.60, and 1.76 . From location B six
samples were taken with the following results 1.76, 1.41, 1.87, 1.49, 1.67,
and 1.81 . It is assumed that the amount of gold in a sample in either location
have a standard normal distribution with a fixed, yet unknown, mean and variance,
and that the variance in both locations is equal. Test the hypothesis that the
mean gold content of both locations is equal. Use a 10% level of significance, in
other words assume that if the two means were the same the test would pass 90% of
the time.
(Answer),
(Solution).
The police commissioner hired a mathematician to help at a crime scene. At the scene were between 100 and 200 glasses of wine. Exactly one glass was poisoned. The police lab could test any sampling for poison. A group of glasses could be tested simultaneously by mixing a sample from each glass. The police commissioner desires only to minimize the maximum possible tests required to determine which exact glass was poisoned. The mathematician started by asking a detective to select a single glass at random for testing. "Wouldn't that waste a test?", the detective asked. "No, besides I'm in a gambling mood.", the mathematician replied. How many glasses were there?
(Answer),
(Solution).
Probability required. A player sits down at a
roulette table with $20. He bets $1 at a time on either red or black.
Either bet pays even money and has a probability of 9/19 of winning.
What is the probability that the player wins $10 before losing all of
his $20?
(Answer),
(Solution).
The keeper of the web page
The premature death of rockstars argues that rockstars rock stars
do not live as long as the general population. He states that the average
age at death of rock stars is 36.9 and 75.8 for the general population.
What is wrong with this use of these statistics? This is an illustrated
example of lying with statistics.
(Answer).
Thirteen pirates put their treasure in a safe. They decide that the safe should be able to be
opened if any majority of pirates agree but not be able to be opened if any minority
agree. The pirates don't trust
each other so they consult a locksmith. The locksmith puts a specific number of locks on
the safe such that every lock must be opened to open the safe. Then he distributes keys
to the pirates such that every pirate has some but not all of the keys. Any given lock can
have multiple keys but any given key can only open one lock. What is the least number of
locks required?
(Answer),
(Solution).
A round table sits flush in a corner of a square room. One point on the
edge of the table is 5" from
one wall and 10" from the other. What is the radius of the table?
(Answer),
(Solution).
What is the expected number of turns needed to form a Yahtzee.
(Answer),
(Solution).
