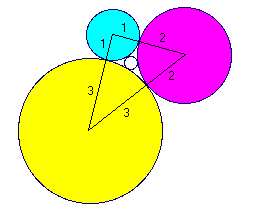
The triangle marked by the centers of the three outer circles conveniently forms a right triangle with sides 3, 4, and 5 (32 + 42 = 52) as seen by the diagram below.
Next draw segments from the center of the interior circle and perpendicular to the outer triangle sides of length 3 and 4.
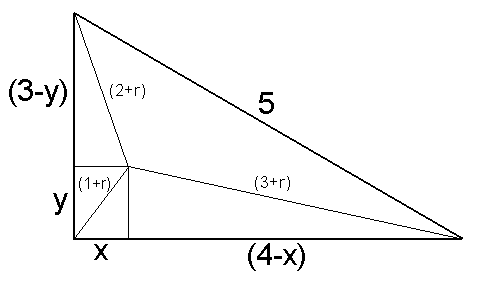
There are four right triangles in this picture, two of which are the same. Using the pythagorean formula we know:
(1): x2 + y2 = (1+r)2
(2): x2 + (3-y)2 = (r+2)2
(3): y2 + (4-x)2 = (r+3)2
Combining equations (1) and (2) we get y=(3-r)/3
Combining equations (1) and (3) we get x=(2-r)/2
Substituting these values for x and y back into equation 1 we get:
((2-r)/2)2 + ((3-r)/3)2 = r2 + 2r + 1
This leads to...
23*r2 + 132r - 36 = 0
Putting this through the quadratic formula we get r=6/23, -6
So the interior circle has radius 6/23 and the outer circle has radius 6.
Here is my old solution, as well as some comments from another reader.
The solution to this problem is rather hard to explain so I'm only going to go over it briefly.
First arrange two of the circles so that their centers lay on the y axis. Then use your trigonomtry to determine the coordinates of the center of the third circle (2.4,-.2) if the large circle is on top, the middle circle on bottom, and the third circle is to the right. See problem 92 for help in how to find such coordinates.
Second, invert all three circles such that the third circle is mapped onto itself. Note that the top and bottom circles are mapped to a horizontal lines that are tanjent to the third circle.
Note: To invert any figure take all points (t,r) and map them onto the point (t,c/r) where t is the angle in polor coordinates and r is the distance from the center. In this case choose the constant c carefully such that the third circle is mapped onto itself (okay, c=4.8 in this case).
The image of the center circle will be tanjent to both horizontal lines and the third circle. Going to the right of the third circle will lead us to the interior circle.
Consider the line that goes through (0,0) and the center of the circle in the above step. The distance from the center of the points where this line intersect the circle are sqr(19.4)-1 and sqr(19.4)+1. Invert these two points and their distance from the center are 4.8/(sqr(19.4)-1) and 4.8/(sqr(19.4)+1). Both these points lay on a diameter of the interior circle so take their difference and divide by 2 to get the radius. The answer simplifies to 6/23.
To find the exterior solution shift the third circle to the left rather than the right. The radius of the exterior solution is exactly 6!
Note: The general case if the third circle has coordinates (x,y) and radius r then the radii of the solution circles are (x2 + y2 - r2) / (4xr +/- (x2+y2+3*r2)).
The + will determine the interior solution, the - the exterior solution.
I would like to propose a solution, also using some trigonometry. First of
all, some definitions:
The centres of the four circles:
'A' for radius 3.
'B' for radius 2
'C' for radius 1
'Z' for the middle circle.
Two angles:
'a' between CA and CZ
'b' between CB and CZ
Our unknown:
'x' is the radius of the middle circle
Then, we make some obvious statements:
CA = 1 + 3 = 4
CB = 1 + 2 = 3
AB = 2 + 3 = 5
AZ = 3 + x
BZ = 2 + x
CZ = 1 + x
Followed by a trivial consequence:
(1) a + b = PI/2 (because CA^2 + CB^2 = AB^2)
Now we establish two equations using trygonometry:
(2) BZ^2 = CZ^2 + CB^2 - 2*CZ*CB*cos(b)
(3) AZ^2 = CZ^2 + CA^2 - 2*CZ*CA*cos(a)
By replacing the values we know and introducing 'x', (2) and (3) become:
(2) (2 + x)^2 = (1 + x)^2 + 9 - 2*3*(1 + x)*cos(b)
(3) (3 + x)^2 = (1 + x)^2 + 16 - 2*4*(1 + x)*cos(a)
By expanding the squares and simplifying (I also omit some '*' to make the
formulae more readable) we obtain:
(2) -6 + 2x + 6(1 + x)cos(b) = 0
(3) -8 + 4x + 8(1 + x)cos(a) = 0
By adding '+2 -2' to the left side of (2) and '+4 -4' to the left side of
(3), and then grouping '(1 + x)' terms, we obtain:
(2) (1 + x)(1 + 3cos(b)) = 4
(3) (1 + x)(1 + 2cos(a)) = 3
>From (1), we can express cos(a) in terms of cos(b):
(1) cos(a) = cos(PI/2 - b) = sin(b) = sqrt(1 - (cos(b)^2))
By substituting cos(a) in (3):
(3) (1 + x)(1 + 2sqrt(1 - (cos(b)^2))) = 3
Now we can calculate cos(b) from (2) and substitute it into (3):
(2) cos(b) = (4/(1 + x) - 1)/3 ==>
(3) (1 + x)(1 + 2sqrt(1 - ((4/(1 + x) - 1)/3)^2)) = 3
For better reading, we can define y = 1/(1 + x), with which (3) becomes (we
can multiply both sides by (1 + x) because x > 0; therefore, (1 + x) > 0 too):
1 + (2/3)sqrt(9 - (4y - 1)^2) = 3y
A bit of simple algebra brings us to:
4sqrt(2 + y - 2y^2) = 9y - 3
We will verify later that '(2 + y - 2y^2) >= 0'. For the time being, we
square both sides and we get (after some simplification):
145y^2 - 86y -23 = 0
This resolves into: (43 +- 72)/145. By taking the positive solution, we
obtain:
y = 23/29 ==> x = 29/23 - 1 = 6/23.
To check that '2 + y - 2y^2 >= 0', we calculate:
2 + y - 2y^2 = 2 + 23/29 - 2(23/29)^2 = 1.5+ > 0
I haven't worked on the "external" circle (yet), and my solution relies on
the fact that the centres of the original circles form a right triangle.
You do show a more general solution, but I confess (please, do not take
offense) that I am a bit skeptical that such a simple equation would apply.
In fact, I did not manage to understand it. Perhaps (time permitting), you
could add an explanatory figure.
You say that the two centres A and B are along the Y-axis. What you don't
say is that the X-axis is the tangent between the two bigger circles. This
implies the two following equations (C must be below the X-axis, because
the biggest circle is above it. Therefore, we can write the formulae in
such a way that y calculates to a negative number):
(1) BC^2 - (2 + y)^2 = x^2
(2) AC^2 - (3 - y)^2 = x^2
This system provides x = 2.4 and y = -0.2, which is what you say in your
solution.
So far so good, but then I really get lost...
Ciao, Giulio
Michael Shackleford, A.S.A.