Problem 43 Solution

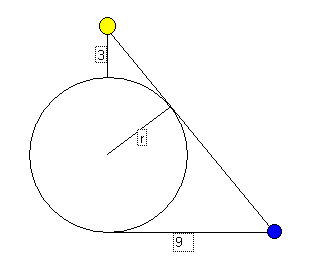
Let a be the angle between the line from the yellow house to the north gate and the line from the yellow house to the blue house.

sin(a) = r/(r+3)

tan(a) = 9/(2r+3)

cos(a) = sqr(1-sin²(a)) = sqr(1-sin²(r/(r+3))) = sqr(6r+9)/(r+3)

tan(a) = sin(a)/cos(a) = (r/(r+3)) * ((r+3)/sqr(3*(2r+3))) = r/sqr(3*(2r+3))

Equating the two expressions for tan(a):

9/(2r+3) = r/sqr(3*(2r+3))

9 * sqr(3) * sqr(2r+3) = r*(2r+3)

9 * sqr(3) = r * sqr(2r+3)

243 = r²*(2r+3)

2r³ + 3r² - 243 = 0

A visit to The MathServ Calculus Toolkit will factor this to (2r-9)*(r² + 6r + 27) = 0.

The real solution is r=4.5

Here are two more solutions presented by Heng Cheng Suang:

I would like to suggest another soln to problem 43.
- just by using pythagoras thm (and/or similar triangles)
  the solution may be solved too.

Let the triangles be labelled as

        A
        |\
        | \E          It is noted that angle AED is 90 deg,
        | /\          and EC is 9 units (properties of tangents)
        |/  \
       D|    \
        |     \    
        --------
        B       C      


USING ONLY PYTHAGORAS THM
-------------------------------------------------------------------------
        
Based on triangle AED (By pyt. thm.),                           STEP 1

             AE = sqrt[(3+r)^2 - r^2)] = sqrt(9+6r)

Based on triangle ABC (By pyt. thm.),                           STEP 2

             (3+2r)^2 + 9^2 = [sqrt(9+6r) + 9]^2
Solving                                                         STEP 3
             4r^4 + 12r^3 + 9r^2 - 486r - 729 = 0
                                            r = 4.5


                                   OR 

-------------------------------------------------------------------------
USING SIM TRIANGLES PROPERTIES
-------------------------------------------------------------------------
STEP 1 same

STEP 2 is replaced by
             9 / (3 + 2r)   = r / sqrt (9 + 6r)              
            
STEP 3 same

I would like to thank Elliot Hunter for suggesting this problem which originally appeared the the November 1937 issue of Popular Science Monthly. The solution is by Dr. Anthony of the math forum.