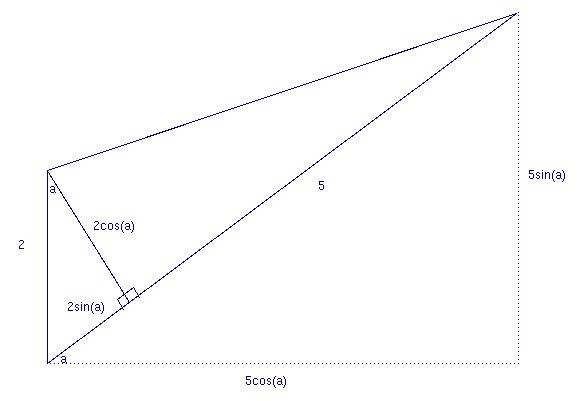
First reword the problem such that the coordinates of the bird's initial position are (100,0) and the nest is at (0,0). In polar coordinates the inital position of the bird is (100,0o). Let p stand for the distance to the origin in polar coordinates, and let a stand for the angle.
Considering that the bird always flied towards the nest (p direction) and the wind blows north (y direction) the following graph shows the change in the variables with respect to a change of one infinitesimal unit of time in units of time. Note that as an angle approaches zero its arc approaches a straight line.

(1) dp/dt = -5 + 2sin(a).
(2) da/dt = 2cos(a)/p.
(3) dx/dt = -5cos(a).
(4) dy/dt = 2 - 5sin(a).
Divide eq. (3) by eq. (2):
(5) dx/da = (dx/dt)/(da/dt) = -5pcos(a)/2cos(a) = -5p/2 = -(5/2)*(x/cos(a)). (see graph above)
Rearrange:
(6) (2/x)dx = (-5/cos(a))da.
Integrate both sides:
(7) ln(x2) = -ln(sec(a)+tan(a))5 + C you might need an integral table for the integral of 1/cos(a).
Exp() both sides:
(8) x2*(sec(a) + tan(a))5 = C.
Put in the intial condition of x=100, a=0 to solve for the constant:
(9) x2*(sec(a) + tan(a)) = 10,000.
(sec(a) + tan(a))5 = (100/x)2.
(sec(a) + tan(a)) = (100/x)2/5.
Let b=(100/x)2/5, then:
(10) sec(a) + tan(a) = b.
(11) (1+sin(a))/cos(a) = b (sec(a)=1/cos(a), tan(a)=sin(a)/cos(a)).
(12) (1+(1-cos2(a))1/2) / cos(a) = b.
1+(1-cos2(a))1/2 = b*cos(a).
(1-cos2(a))1/2 = b*cos(a) - 1.
1-cos2(a) = b2*cos2(a) - 2*b*cos(a) + 1.
2*b*cos(a) = (1+b2)*cos2(a).
2*b = (1+b2)*cos(a).
(13) cos(a) = 2*b / (1+b2).
Substitute equation (13) into equation (3):
(14) dx/dt = -5*cos(a) = -10*b / (1+b2).
Rearranging:
dt = -(1+b2)/(10*b) dx.
-10 dt = b+(1/b) dx
(15) -10 dt = (100/x)2/5 dx + (x/100)2/5 dx, remember b=(100/x)2/5
Integrating:
(16) Constant -10t = (5/3)*1002/5*x3/5 + (5/7)*(1/100)2/5*x7/5.
Put in the initial constants t=0 and x=100:
Const = (5/3)*1002/5*1003/5 + (5/7)*(1/100)2/5*1007/5.
Const = (5/3)*100 + (5/7)*100 = 5000/21.
So the function of x and t is:
(17) 5000/21 - 10t = (5/3)*1002/5*x3/5 + (5/7)*(1/100)2/5*x7/5.
The original question was how long does it take the bird to reach the nest, in other words what is t when x=0. By substituting x=0 in the above equation t = Const/10 = 500/21.
Tristan Simbulan sent in the following solution which you may find better:
The initial position of the bird is ( 100, 0 ) and the nest is ( 0, 0 ) I am using the velocity vector component parallel to y and x.
Let a be the angle between x axis and bird's line of sight towards ( 0, 0 ).
(1)The wind velocity minus y component of the bird's velocity = dy/dt = 2 - 5 sin a = 2 - 5 * y/sqrt(x^2 + y^2)
(2) Velocity x component = dx/dt = - 5 cos a = - 5 * x / sqrt( x^2 + y^2 )
(3) (dy/dt)/(dx/dt) = dy/dx = [ 5y -2 * sqrt(x^2 + y^2) ] / 5x 5xdy - 5ydx + 2 * sqrt(x^2 + y^2) dx = 0 Let y = vx, dy = vdx + x dv , the result by substitution is dv/sqrt(1 + v^2) + 2/5 * dx/x = 0.
ln[ v + sqrt(1 + v^2) ] + 2/5 ln x = C since v = y/x, by substitution ln [ y/x + sqrt(1 + y^2/x^2) ] + 2/5*ln x = C At y = 0 and x = 100 , then C = ln 100^(2/5).
The equation of the curve is sqrt(x^2 + y^2) = x^(3/5) *100^(2/5) - y.
Square both sides then y = [ 100^(4/5) * x^(3/5) - x^(7/5) ] / [ 2 * 100^(2/5)].
Solve (2) Velocity x component = dx/dt = - 5 cos a = - 5 * x / sqrt( x^2 + y^2 ) in terms of y.
By algebraic manipulation using fractional exponent and factoring the result is 100^(4/5) * x^(-2/5) dx + x^2/5 dx = - 10^(9/5) dt 5/3 *100^(4/5) * x^(3/5) + 5/7 * x^(7/5) = - 10^(9/5) * t + C At x =100 and t = 0 , C = 100^(7/5) * 50/21.
At x = 0 the result is 0 = - 10^(9/5) * t + C , substitute C = 100^(7/5) * 50/21 Solve: 10^(9/5)*t = 100^(7/5) * 50/21.
Therefore t = [100^(7/5)] / [10^(9/5)] * 50/21
t = [ 10^(14/5) ] / 10^(9/5) * 50/21 = 10 *50/21 = 500/21.
Go back to Problem 55
Go back to Shack's Math Problems
Michael Shackleford, A.S.A.