Country x is planning to attack country y, and country y is anticipating the attack. Country x can either attack by land or by sea. Country y can either prepare for a land defense or a sea defense. Both countries must choose either an all land or all sea strategy, they may not divide their forces. The following are the probabilities of a successful invasion according to both strategies used.
- If x launches an attack by sea and y prepares a defense by sea the probability of a successful invasion is 80%.
- If x launches an attack by sea and y prepares a defense by land the probability of a successful invasion is 100%.
- If x launches an attack by land and y prepares a defense by land the probability of a successful invasion is 60%.
- If x launches an attack by land and y prepares a defense by sea the probability of a successful invasion is 100%.
What should the strategy of country x be, assuming the goal is to maximize the probability of a successful invasion? Assume the goal of country y to be to minimize the probability of a successful invasion. What is the final probability of a successful invasion assuming both utilize an optimal strategy? (Hint), (Answer), (Solution).
Probability required.
What is the probability of winning a bet on the pass line in craps? If
you aren't familiar with the bet click here.
(Answer),
(Solution).
Probability required.
You and your partner in crime are both arrested and questioned
separately. You are offered a chance to confess, in which you
agree to testify against you partner, in exchange for all
charges being dropped against you, unless he testifies
against you also. Your lawyer, whom you
trust, says that the evidence against both of you, if neither
confesses, is scant and you could expect to take a plea and
each serve 3 years. If one implicates the other, the other
can expect to serve 20 years. If both implicate each other
you could each expect to serve 10 years. You assume the
probability of your partner confessing is p. Your highest
priority is to keep yourself out of the pokey, and your
secondary motive is to keep you partner out. Specifically
you are indifferent to you serving x years and your partner
serving 2x years. At what value of p are you indifferent to
confessing and not confessing?
(Answer),
(Solution).
No math required.
In front of you are 12 pearls, 11 being real and one fake. The
real ones all weigh the same and the fake one differs in weight
from the real ones (may weigh more or less). With a balance
scale and three weighings how can you weed out the fake one and
determine whether it is too heavy or too light?
(Answer & Solution).
No math required.
Five pirates have come across a treasure of 1000 coins. According
to pirate rules the pirate of highest rank must make a suggestion
on how to divide the money. If a majority agree to his suggestion
then it is to be followed by all the pirates. However, if the suggestion
does not get a majority approval then the suggesting pirate is thrown
overboard, after which time the remaining pirate of highest rank then makes
a suggestion under the same rules. This process repeats, if
necessary, until only the pirate of lowest rank is left, in which case
he would get everything. Any pirate may suggest any distribution,
rank does not guarantee getting more coins than anybody else. Assume
that all pirates are infinitely greedy, infinitely logical, and infintely
bloodthirsty, and that each pirate knows this to be true of every other pirate.
The highest priority of each pirate is to get as much money for themselves as
possible. The second highest priority is to throw overboard the other pirates.
A pirate will vote to throw another one over even if they have no monetary gain
by doing so, and even if it would cost them their own life, but would not if
throwing them over would cost even 1 coin. How should the first pirate suggest
dividing the money?
(Answer),
(Solution).
Partial differential equations required.
You invest $1 in a bank account. At time t the interest rate on this account is
t. Interest is compounded infinitely? How much will be in the account after
x years?
(Answer),
(Solution).
Integral calculus required.
An airplane weighs 10,000 pounds, has a 1000 gallon tank, burns fuel at a
rate of 5 gallons per minute, and has a speed in miles per hour of 6,000,000
divided by the sum of weight of the plane and remaining fuel. Each gallon of
fuel weighs 10 pounds. With a full tank how far can the plane fly?
(Answer),
(Solution).
Logic required.
How can three surgeons, with open wounds on their hands, operate on a patient
with only two surgical gloves so that nobody is directly exposed to anybody
else's blood?
(Answer).
Probability required.
What is the player's advantage in craps if the player will bet
the pass line and take double odds if a point is rolled. If you aren't familiar with
the game go here.
(Answer),
(Solution).
Algebra, interest theory required.
Given a $100,000 mortgage, a payment period of 30 years, monthly payments (the first
due at the end of the first month), and an interest rate of 7.5% compounded monthly,
what will be the monthly payments?
(Hint),
(Answer),
(Solution).
Probability required.
In the game of keno the casino chooses 20 numbers at random from 1 to 80,
without repeating any number. The player guesses x numbers from 1 to 80
(where x<=20).
What is the probability that the player gets y numbers correct (where
y<=x)? In other words what is the probability that y numbers are in common
to both those chosen by the casino and the player?
(Answer).
Geometry required. In the diagram above AB=3, BC=7, and AC=9. What is BD? (Answer), (Solution).
Simplify ei (ei*pi for Netscape users).
(Hint),
(Answer),
(Solution).
Any given length of highway is equally likely to have as many potholes as any other length of
equal size. The average number of potholes per mile of highway is 3. What is the probability
that 2 miles of highway have 3 or fewer potholes?
(Answer),
(Solution).
Four people need to cross a bridge at night. The bridge is only strong enough to hold at
most two people at once. Because it is night a flashlight must be used for all crossings.
It takes person A ten minutes to cross, person B five minutes, person C two minutes, and person D
one minute. If two cross at the same time they must walk at the slower man's pace. How can you
get everyone across in 17 minutes?
(Answer & Solution).
Three people (A, B, and C) need to cross a bridge. A can cross the bridge in 10 minutes, B can cross in 5
minutes, and C can cross in 2 minutes. There is also a bicycle available and any person
can cross the bridge in 1 minute with the bicycle. What is the shortest time that all men
can get across the bridge? Each man travels at his own constant rate.
(Hint 1),
(Hint 2).
(Answer),
(Solution).
Geometry, integral calculus required.
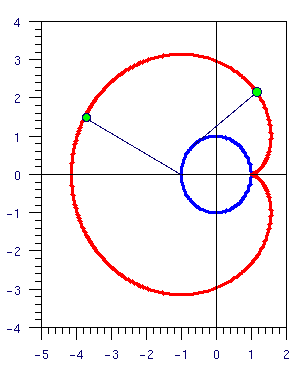
A dog is chained to a point of the side of a circular lighthouse of radius 1. The length of the dog's chain is pi. The dog may not go inside the lighthouse. How much area can the dog cover? (Answer), (Solution).
You are to form five rectangles using each integer once from 1 to 10 as the lengths of
the sides. How can you tile a square, without overlapping, with the five rectangles?
There are four possible answers.
(Answer),
(Solution).
It is your task to deliever as much grain as possible from city A to city B. The
cities are 1,000 miles apart. You initially have 10,000 pounds of grain. Your
camel may carry up to 1,000 pounds and eats 1 pound
of grain per mile traveled. You may leave grain along the way and
return to it later. How much grain can you deliever to city B?
(Answer),
(Solution).
Basic geometry required.Basic math required.
