Probability required.
Suppose you have a coin in which the probability of flipping a heads is p, where p>=0.5 .
What is the expected number of flips it will take for the number of heads to equal
the number of tails, assuming the first flip is a tails?
(Answer),
(Solution).
Probability required.
Given an ordinary deck of cards, what is the probability of drawing each kind
of hand in poker? No discards, just the first five cards. Remember, aces
can be high or low.
(Answer),
(Solution).
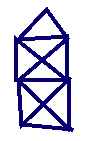
No math required. It is impossible to draw this figure without taking the pen off the paper, redrawing any lines, or other trickery. Explain why it is impossible. (Answer & Solution).
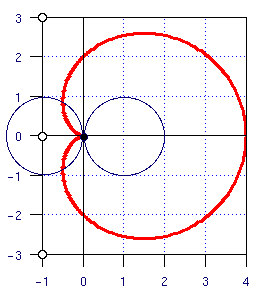
Integral calculus and trigonometry required. Two circles of radius one are adjancent at point (0,0). Let the center of the first circle be at point (-1,0). Label the point on the edge of the first circle at (0,0) x. The second circle is centered at (1,0). Rotate the first circle around the second, like a gear, keeping the second circle stationary. If you traced the path of point x as the first circle traveled around the second what would be the length of the path point x traced? The figure above shows the path in red. (Answer), (Solution).
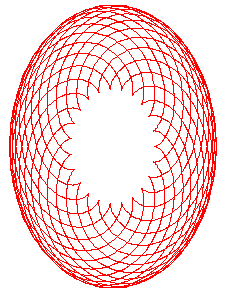
Modular arithmetic suggested. In a spirograph toy you first select two circular gears. Keeping one gear stationary, you let the second gear travel around the first one until it arrives back at its initial position and orientation. By tracing the path with a pen through a hole in the second gear you can make designs like the one above. Assuming the notches in the gears are equally spaced apart, and that there are x notches in the stationary gear, and y notches in the moving gear, how many trips around the first gear will the second gear need to make before it arrives back at its initial position and orientation? (Answer).
Advanced geometry requied.
Assuming the earth earth is spherical with radius r. What is the shortest distance
along the surface from point A to point B. Let p1 and p2 be
the two longitudes, measured from 0 to 2*pi. Let q1 and q2 be
the two latitudes, measured from 0 to pi, where 0=north pole and pi=south pole.
(Answer),
(Solution).
Probability required.
In blackjack if the dealer is showing an ace you make "take insurance" or
bet that his/her other card is a ten. A winning bet pays 2:1 (win $2 for
every $1 bet, keeping original bet). What is the house advantage in
this bet? How many non-tens would you have to remove from a single deck
game to make it a fair bet? Assume you know nothing about the cards
that have already been played (including the dealer's ace and your own).
(Answer),
(Solution).
What is the expected return of this game?
(Answer),
(Solution).
Using a balance scale and four weights you must be able to balance
any integer load from 1 to 40. How much should each of the four
weights weigh?
(Answer).
Integral calculus required.
The object of a game is to come as close to 1 point as possible without
going over. On a player's first turn he is given a random number of
points, taken from a uniform distribution from 0 to 1. He may then
keep that number, or take another from the same distribution, adding the
second number of the first. The second player, knowing the first
player's score, takes one number and has a chance for a second. Assuming
the first player follows an optimal strategy in determining whether or
not to take a second number, what is the probability that the first player
will win? You may express your answer in terms of x, where x3
+ 3x2 - 1 = 0. (Note that this game is the same as the Showcase
Showdown in The Price is Right, only using a wheel with an infinite
number of intervals).
(Answer),
(Solution).
Probability required.
In the "Match 5" game of the Maryland state lottery the player chooses any five numbers
from 1 to 39. At a designated time there will be a drawing in which five numbers
from 1 to 39 will be drawn at random, plus a "bonus ball" from the remaining 34. The
following is the payout schedule for a $1 ticket plus an example of a winning ticket
given that the numbers drawn were 1-2-3-4-5, with a bonus number of 6:
You have nine pearls, eight are real and one is fake. All the
real ones weigh the same and the fake weighs less than
the real ones. Using a balance scale twice how can you weed out
the fake one?
(Answer).
Algebra required.
A jar begins with one amoeba. Every minute, every amoeba
turns into 0, 1, 2, or 3 amoebae with probability 25%
for each case ( dies, does nothing, splits into 2, or splits
into 3). What is the probability that the amoeba population
eventually dies out?
(Answer),
(Solution).
Algebra and probability required.
There is a free gift in my breakfast cereal. The manufacturers say that
the gift comes in four different colors, and encourage one to collect
all four (thus eating lots of cereal). Assuming there is an equal
chance of getting any one of the colors, what is the expected number
of boxes I must consume to get all four?
(Answer),
(Solution).
Algebra and probability required.
What is the answer for the above problem, only instead of 4 different prizes
there are n different prizes.
(Answer),
(Solution).
Probability required.
Suppose there are n people in an office. At Christmas they have a random
gift exchange in which every name is writen on scraps of paper, mixed around
in a hat, and then everyone draws a name at random to determine who they are
to get a gift for. What is the probability nobody draws their own name?
(Answer),
(Solution).
Probability required.
You choose one of two identical looking bags at random. One bag has three
black marbles and one white marble. The other has three white marbles and
one black marble. After choosing a bag you draw one marble out at random.
You notice it is black. You then put it back and draw another marble out of
the same bag at random. What is the probability that the second marble drawn is black?
(Answer),
(Solution).
Integral calculus and probability required.
Assume that a pregnant woman's probability of giving birth to a girl is p, where
p is determined at the mother's birth according to a uniform distribution from 0.4 to
0.6 . If the woman's first child is a girl what is the probability her next
child will also be a girl?
(Answer),
(Solution).
Basic math required.
If it takes Bill 20 hours to paint a house and it takes George 30 hours, how long
will it take if they work together yet independently?
(Answer),
(Solution).
No math required.
One one side of a river are three humans, one big monkey, two small
monkeys, and one boat. Each of the humans and the big monkey are
strong enough to row the boat. The boat can fit one or two bodies
(regardless of size).
If at any time at either side of the river the monkeys outnumber
the humans the monkeys will eat the humans. How do you get everyone
on the other side of the river alive?
(Answer&Solution),
You are blindfolded before a table. On the
table are a very large number of pennies. You are told 128 of the pennies
are heads up and the rest are tails up. How can you create two subgroups of pennies,
each with the same number of heads facing up? (Answer)
