You are the foreman in charge of license plate production. Your equipment can produce two different gauges of steel, one weighing about 90% of the other. Normally you use the heavier gauge but one week you leave that responsibility to someone else who sets the gauge randomly every day. After a week you realize that some days the license plates may have been made of the lighter gauge steel. Every days license plates are kept in separate piles. You may use a digital scale once which will give an exact weight of whatever you decide to weigh. Assume that the heavy gauge license plates weigh 1 unit each and the light ones 0.9 units each. You may use the scale only once. How many license plates from each pile should you put on the scale?(Answer).
Two brothers share a flock of x sheep. They take the sheep to the market and sell each sheep for $x. At the end of the day they put the money from the sales on the table to divide it equally. All money is in $10 bills, except for less than ten excess $1 bills. One at a time they take out $10 bills. The brother who draws first also draws last. The second brother complains about getting one less $10 bill so the first brother offers him all the $1 bills. The second brother still received a total less than the first brother so he asks the first brother to write him a check to balance the things out. How much was the check?
(Answer),
(Solution).
You are traveling down a path and come to a fork in the road. A
sign lays fallen at the path indicating that one path leads to
a village where everyone tells the truth and the other to a village
where everyone tells lies. The sign has been knocked down so you
do not know which path leads to which village. Then someone from
one of the villages (you don't know which one) comes down the path
from which you came. You may ask him one question to determine which
path goes to which village. What question do you ask?
(Answer),
(Solution).
You need to warm milk in a baby bottle from its initial temperature of
15 degrees centigrade to 25 degrees. You put the bottle in a
pot of boiling water which stays at constant temperature of
100 degrees. The thickness and conductivity of the bottle
are such that the initial rate of heat transfer is 85 degrees
per minute. However heat transfer is proportional to the
difference between the temperature of the milk and the
water. How many minutes will it take to heat the bottle to
25 degrees?
(Answer),
(Solution).
Person x and y have the following conversation:
x: I forgot how old your three kids are.
y: The product of their ages is 36.
x: I still don't know their ages.
y: The sum of their ages is the same as your house number.
x: I still don't know their ages.
y: The oldest one has red hair.
x: Now I know their ages!
How old are they? (Answer), (Solution).
The king has 100 young ladies in his court each with
an individual dowry. No two dowrys are the same. The
king says you may marry the one with the highest dowry if
you correctly choose her. The king says that he will
parade the ladies one at a time before you and each will
tell you her dowry. Only at the time a particular lady
is in front of you may you select her.
The question is what is the strategy that maximizes your
chances to choose the lady with the largest dowry?Hint: You should let x ladies go by and choose the first one with a dowry greater than the maximum of the first x. Of course you will pass the highest one if she is among the first x, but that is part of the game. (Answer), (Solution).
There is a 6 foot wide alley. Both walls of the alley
are perpendicular to the ground. Two ladders, one
10 feet long, the other 12 feet, are propped up from
opposite corners to the adjacent wall, forming an
X shape. All four feet of each ladder are firmly
touching either the corner or the wall. The two ladders
are also touching each other at the intersection of the
X shape. What is the distance from the point of
intersection to the ground?
(Answer),
(Solution).
A factory that produces tables and chairs is equipped with 10 saws, 6 lathes, and 18
sanding machines. It takes a chair 10 minutes on a saw, 5 minutes on a lathe, and 5
minutes of sanding to be completed. It takes a table 5 minutes on a saw, 5 minutes on a
lathe, and 20 minutes of sanding to be completed. A chair sells for $10 and a table
sells for $20. How many tables and chairs should the factory produce per hour to yield
the highest revenue, and what is that revenue?
(Answer),
(Solution),
Four dogs occupy the four corners of a square with side of length a. At the same time each
dog starts walking at the same speed directly toward the dog on his left. Eventually all four dogs
will converge at the center of the square. What path does each dog follow and what is the
distance each dog walks until he reaches the center?
(Answer),
(Solution).
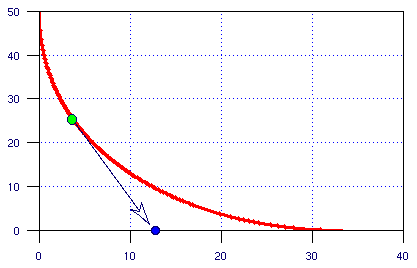
Partial differential equations required. There is a boat traveling east at a speed of 20 kilometers per hour. A second boat is 50 kilometers directly north of the first boat at time t=0. The second boat can travel at a speed of 30 kilometers per hour. The direction of the second boat at all times is such that the first boat is directly in front of it. You may assume the earth is flat for the purposes of this problem.
What path does the second boat take and at what time will it intercept the first boat?
In the graph above the speed of the fast boat (green) is 2 kph, and the speed of the slow boat (blue) 1 kph. I changed the parameters because I didn't want to give away the answer in the graph. (Answer), (Solution)
Calculus required.
What is the value of $1, invested for one year at 100% interest,
compounded infinitely?
(Answer),
(Solution).
You have a 6 foot fence and at 15 foot board. The sun is shining directly overhead.
You want to lean your board against the fence so that as large a shadow as possible
covers your neighbor's yard. What is the maximum length of the shadow you can
form? The ladder must rest against the fence and touch the ground on your side of
the fence.
(Answer),
(Solution).
Knowledge of infinite series required.
Assuming both players take turns what is the probability the player who
goes first will lose at Russian roulette using a gun with six chambers?
(Answer),
(Solution).
10% of the people in a certain population use an illegal drug. A drug test yields
the correct result 90% of the time, whether the person uses drugs or not. A random
person is forced to take the drug test and the result is positive. What is the
probability he uses drugs?
(Answer),
(Solution).
Calculus and knowledge of the exponential distribution requied.
You have ten light bulbs. Five have an average life of 100 hours, and the
other five have a average life of 200 hours. These light bulbs have a
memoryless property in that their current age (measured in how long
they have already been on) has no bearing on their future
life expectancy. Assuming they are all already on what is the expected
number of hours before the first one burns out?Hint: The density function for this kind of light bulb with average life of n hours is f(x)=1/n * e-x/n. (Answer), (Solution).
Calculus and knowledge of the exponential distribution requied.
In the above problem what is the probability a light bulb with 100 hour
life expectancy burns out first?
(Answer),
(Solution).
What is the minimum number of people do you need, chosen at random, so that there is at
least a 50% chance that at least two have the same birthday. Assume that people are
born randomly throughout the year. You may ignore leap day.
(Answer),
(Solution).
Two people arrive in a restaurant independently. Each arrives a random time between
5pm and 6pm, distributed uniformaly (no moment in this range is any more likely for
arrival than another). What is the probability they arrived within 10 minutes of
each other?
(Answer),
(Solution).
What is the smallest integer greater than 0 that can be written entirely with zeros and ones and is evenly divisible by 225?
(Answer),
(Solution).
You are in a race in which the starting line is at a certain point on a
straight beach. The finish line is in the water. One way to arrive at
the finish line is to run 4 kilometers down the beach, make a 90 degree
turn and swim 1 kilometer. However, you may cut into the water at
any point. You speed on land is 6 k.p.h and you speed in water is
2 k.p.h.. At what point, measured from the starting line, should
you cut into the water?
(Answer),
(Solution).