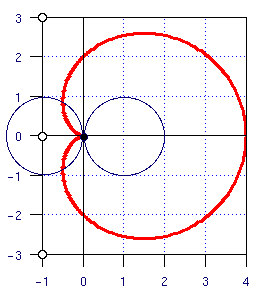
Let a be the distance from the point (0,0) to a point on the figure (known as a cardoid). Next consider the angle t formed from the points (-1,0), (0,0) and a at (0,0).
After working through the trigonomtry (this step is left to you) the length of a in terms of t is 2*(1-cos(t)).
The formula for arc length is the integral of ( a2 + (da/dt)2 )1/2.
In this case it is the integral from 0 to 2*pi of:
( 4*(1-cos(t))2 + 4*sin2(t) )1/2. =
81/2 * (1 - cos(t))1/2.
After consulting a table of integrals we find that the integral of (1 - cos(t))1/2 is -2*21/2*cos(t/2).
Taking the integral the answer works out to 16.
I'd like to thank Andrea for correcting an earlier mistake in my answer.
Michael Shackleford, A.S.A.