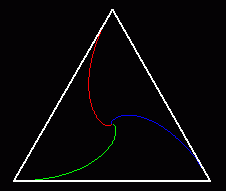
Let C be the center of the square at point (0,0). Let the dogs be at initial points (.5,.5), (.5,-.5), (-.5,-.5), and (-.5,.5). Let dog 1 bet at (.5,-.5) who is chasing dog 2 at (.5,.5). Consider the line from C to dog 1. Next consider the line from dog 1 to dog 2. The angle between these lines is 135 degrees.
Theorem: Let C be a fixed point, D a point on a curve, r the distance from C to D, x the polar angle formed by r, and y the angle formed by the angle between CD and the tangent line to the curve at point D. Then tan(y)=r/(dr/dx).
So the line of sight from the center to the initial point of dog 1 would be be at a 270 degree angle. The line of sight from dog 1 to dog 2 would be a vertical line of 90 degrees. The angle between these lines is 270 degrees. The tangent of 270 is -1. So we have r/(dr/dx) = -1. Thus r(x)=c*e-x.
At the moment the dogs start walking x equals 0. At this moment the distance from the center to any of the dogs is 2-1/2. So r(x)=2-1/2*e-x.
The arc length is given by the formula:
Integral from 0 to infinity of ((f(x))2+(f'(x))2)1/2 =
Integral from 0 to infinity of ((2-1/2*e-x)2 + (-2-1/2*e-x)2)1/2 =
Integral from 0 to infinity of (2-1*e-2x + 2-1*e-2x)1/2 =
Integral from 0 to infinity of e-x =
-e-x from 0 to infinity =
=0 - (-e0) =
0 -(-1) = 1
The path the dogs take is called a logarithmic spiral. It is an interesting paradox that the dogs will make an infinite number of circles, yet the total distance is constant. Every revolution the size of the square will to e-2*pi/21/2 = 0.03055663 times it's size before the revolution.
Suppose dog A is pursuing dog B who is pursuing dog C. During the entire pursuit, the dogs remain at the corners of a square, and angle ABC is a constant 90 degrees. That is, B's path towards C is always perpendicular to A's path towards B, and B has zero velocity in the direction along A's path. Since B neither approaches nor recedes from A during the walk, A simply covers the intial separation of 1.
Antonio Molins went further to state that as dog A is heading direcctly towards dog B, dog B is moving towards from dog A at rate equal to cosine of any of the interior angles of the shape made by the dogs. He also provided the following graphics.
For example consider a pentagon. Remember that for a n-gon of n sides each angle will be 180*(1-(2/n)). So a pentagon will have angles of 108°. Let's assume each dog walks at a rate of 1 unit per minute, where the initial shape has sides of 1 unit. As pointed out by David Wilson we can forget about the spiral paths but instead think of the dogs walking in straight lines. In the case of the penagon for every one unit dog A draw towards dog B's initial position, dog B will draw cos(180°)=-0.309 units towards dog A. The question is, how long will it take for them to meet? Let the answer to that question be t. In t seconds dog A will cover t units, and dog B will cover .309*t units. The total distance traveled by A equals the distance traveled by B plus 1 (the initial separation). So solving for t: t=0.309+1 --> t=1/(1-.309) --> t=1.4472.
Thus the general formula is 1/(1+cos(t)), where t is an interior angle of the shape.

Number of sides = 3
Lengh of initial side = 1
Each angle = 180*(1-(2/3)) = 60°
Length of path = 1/(1+cos(60)) = 1/(1+0.5) = 2/3

Number of sides = 4
Lengh of initial side = 1
Each angle = 180*(1-(2/4)) = 90°
Length of path = 1/(1+cos(90)) = 1/(1+0) = 1

Number of sides = 5
Lengh of initial side = 1
Each angle = 180*(1-(2/5)) = 108°
Length of path = 1/(1+cos(108)) = 1/(1-.309) = 1.4472

Number of sides = 6
Lengh of initial side = 1
Each angle = 180*(1-(2/6)) = 120°
Length of path = 1/(1+cos(120)) = 1/(1-.5) = 2

Number of sides = 10
Lengh of initial side = 1
Each angle = 180*(1-(2/10)) = 144°
Length of path = 1/(1+cos(144)) = 1/(1-.809) = 5.2361
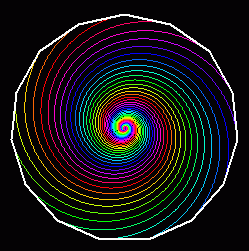
Number of sides = 15
Lengh of initial side = 1
Each angle = 180*(1-(2/15)) = 156°
Length of path = 1/(1+cos(156)) = 1/(1-.9135) = 11.5668