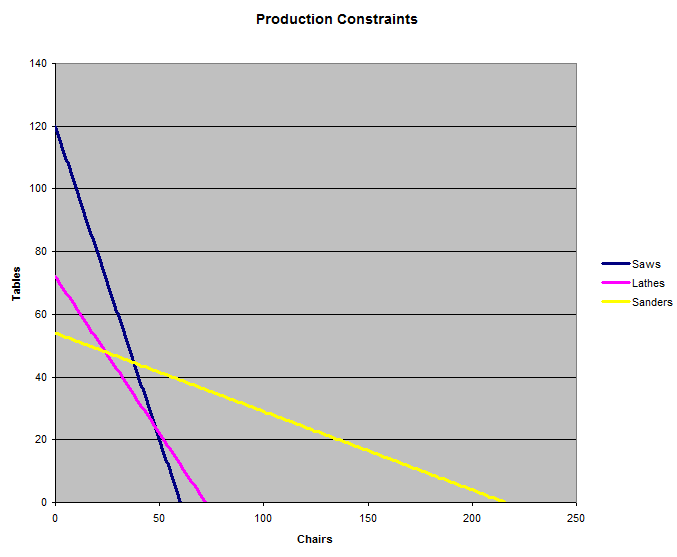
Let c be the number of chairs produced per hour and t the number of tables produced per hour.
The number of saws limit the combination of chairs and tables to 600=10c+5t.
The number of lathes limit the combination of chairs and tables to 360=5c+5t.
The number of sanding machines limit the combination of chairs and tables to 1080=5c+20t.
Next graph these three lines. It should be expected that the answer will lie on the intersection of two of these lines or to make all chairs or all tables. The intersection of the saw and sanding machine line occurs outside of how many chairs the lathe can make so this combination is not a viable answer. The saw and lathe lines cross at 48 chairs and 24 tables. The lathe and sanding machine lines cross at 24 chairs and 48 tables.

Next determine the revenue at all points of intersection.
| Chairs | Tables | Revenue |
| 60 | 0 | 600 |
| 48 | 24 | 960 |
| 24 | 48 | 1200 |
| 0 | 54 | 1080 |
So the optimal answer is to make 24 chairs and 48 tables for revenue of $1200 per hour.
To check it will take 24*10 + 48*5 = 480 minutes of saw time. There are 600 minutes available so the saws will be idle 20% of the time.
It will take 24*5 + 48*5 = 360 minutes of lathe time which is exactly what we have.
It will take 24*5 + 48*20 = 1080 minutes of sanding machine time which is exactly what we have.
I would like to thank Brain Storm for this problem.
Michael Shackleford, A.S.A.