Problem 205 Solution

Question

Imagine a keno game where the numbers are drawn WITH replacement. In other words, 20 balls are drawn from an urn with balls numbered 1 to 80, one at time. As each ball is drawn the number is noted, and then the ball is returned to the urn. The player picks four different numbers from 1 to 80. For each number picked it is considered a match if the casino draws that number at least once. What is the probability for each possible outcome of 0 to 4 matches?

Solution

First determine the probability that the casino will drawn any of the four balls x times, including duplicates. The probability of m such draws is combin(80,m)×(4/80)^m×(76/80)^20-m, where combin(80,x)=80!/(x!×(80-x)!). The following table shows the probability of 0 to 20 total matches.

Table 1 — Total Match Probabilities
Total Matches	Probability
20	9.53674E-27
19	3.62396E-24
18	6.54125E-22
17	7.45703E-20
16	6.02155E-18
15	3.6611E-16
14	1.73902E-14
13	6.60829E-13
12	2.04031E-11
11	5.16878E-10
10	1.08028E-08
9	1.86593E-07
8	2.65895E-06
7	3.10893E-05
6	0.000295348
5	0.002244646
4	0.013327586
3	0.059582148
2	0.188676801
1	0.377353603
0	0.358485922
Total	1

The hard part is determining the probability of d distinct matches given m matching draws. Let's let f(m,d)=probability of d distinct matches, given m total matches.

It is obvious that f(0,0)=1 and f(1,1)=1.

If d=2 then the probability the second matching ball drawn is the same as the first is 1/4. So f(2,1)=0.25, and f(2,2)=0.75.

If d=3 then the probability that the second and third matching balls drawn are the same as the first is (1/4)×(1/4)=1/16. So f(3,1)=0.0625. The probability of three different numbers is (3/4)×(2/4)=6/16=3/8=0.375. The only other possibility is d=2, so f(3,2)=1-0.0625-0.375=0.5625.

If d=4 the probability the probability of only one distinct number drawn is f(4,1)=(1/4)³=1/64. The probability of four distinct numbers is (3/4)×(2/4)×(1/4)=6/64=3/32. Things get a little harder with three distinct mathces. There are 4!/(2!×1!×1!) = 12 ways you can pick one number for the one that is called twice, and two numbers called once. Once you do that there are the same 4!/(2!×1!×1!) = 12 ways you can choose the order of those numbers called. So out of 4⁴=256 ways to pick 4 numbers out of 4, with replacement, 12×12=144 of them result in three distinct numbers. So f(4,3)=144/256=0.5625. By ommission, f(4,2)=1-f(4,1)-f(4,3)-f(4,4)=1-(1/64)-(144/256)-(3/32)=0.328125.

The fun part is calculating the probability of 1 to 4 distinct matches given 5 to 20 total matches. It is fairly obvious that there are 4 (one for each pick) ways out of 4^m matches that all the number can be the same. So the f(m,1)=4/4^m = 1/4^m-1.

For two distinct matches there are combin(4,2)=6 ways to picks two numbers out of the four picks. It would be incorrect to say that f(m,2)=6×(2/4)^m, because it would include, multiple times, the probability of drawing only one number. There are four possible numbers that can be drawn only once, and each of them is triple counted. For example, of the six sets of two numbers: (1,2), (1,3), (1,4), (2,3), (2,4), and (3,4) any given single number appears three times. So, the probability of picking exactly two distinct numbers is 6×(2/4)^m - 4×3×(1/4)^m. Let's look at the case of m=10, for example. f(10,2)=6×(2/4)¹⁰ - 12×(1/4)¹⁰ = 0.005847931.

Things get even messier with three distinct matches. The following equations show that the probability of exactly three matches is the probability of 1-3 matches, less the probability of exactly 2 matches, less the probability of exactly one match.

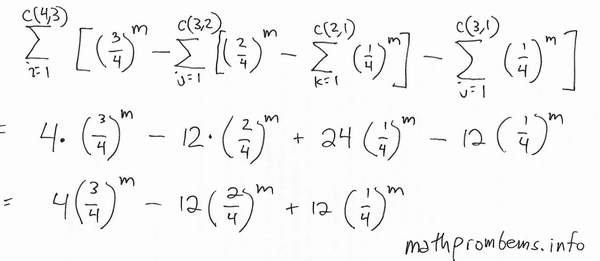
So f(m,3)=4×(3/4)^m - 12×(2/4)^m + 12×(1/4)^m.

For example, for 10 matches, the probability of exactly 3 distinct numbers is 4×(3/4)¹⁰ - 12×(2/4)¹⁰ + 12×(1/4)¹⁰ = 0.213546753.

The probability of exactly four matches can be found by omission, subtracting the probability of 1 to 3 matches from 1.

The following table shows the conditional probability of 0 to 4 matches for 0 to 20 total matches.

Table 2 — Conditional Probability of 0 to 4 Distinct Matches by 0 to 20 Total Matches
Total Matches	Distinct Matches
	4	3	2	1	0
20	0.987320874287	0.012673403675	0.000005722035	0.000000000004	0
19	0.983098313736	0.016890242201	0.000011444048	0.000000000015	0
18	0.977472047671	0.022505064262	0.000022888009	0.000000000058	0
17	0.969977988862	0.029976235237	0.000045775669	0.000000000233	0
16	0.960001168773	0.039907280356	0.00009154994	0.000000000931	0
15	0.946729257703	0.053087644279	0.000183094293	0.000000003725	0
14	0.929094403982	0.070539414883	0.000366166234	0.000000014901	0
13	0.905703306198	0.093564391136	0.000732243061	0.000000059605	0
12	0.874759197235	0.123776435852	0.001464128494	0.000000238419	0
11	0.833988189697	0.163084030151	0.002926826477	0.000000953674	0
10	0.780601501465	0.21354675293	0.005847930908	0.000003814697	0
9	0.711364746094	0.276947021484	0.011672973633	0.000015258789	0
8	0.622924804688	0.353759765625	0.023254394531	0.000061035156	0
7	0.5126953125	0.44091796875	0.046142578125	0.000244140625	0
6	0.380859375	0.52734375	0.0908203125	0.0009765625	0
5	0.234375	0.5859375	0.17578125	0.00390625	0
4	0.09375	0.5625	0.328125	0.015625	0
3	0	0.375	0.5625	0.0625	0
2	0	0	0.75	0.25	0
1	0	0	0	1	0
0	0	0	0	0	1

To get the total probability of 0 to 4 distinct matches, take the dot product of m total matches by the conditional probability of d distinct matches. The following table shows the results.

Table 3 — Total Probability of 0 to 4 Distinct Matches by 0 to 20 Total Matches
Total Matches	Distinct Matches
	4	3	2	1	0
20	0	0	0	0	0
19	0	0	0	0	0
18	0	0	0	0	0
17	0	0	0	0	0
16	0	0	0	0	0
15	0	0	0	0	0
14	0	0	0	0	0
13	0.000000000001	0	0	0	0
12	0.000000000018	0.000000000003	0	0	0
11	0.000000000431	0.000000000084	0.000000000002	0	0
10	0.000000008433	0.000000002307	0.000000000063	0	0
9	0.000000132736	0.000000051676	0.000000002178	0.000000000003	0
8	0.000001656327	0.00000094063	0.000000061832	0.000000000162	0
7	0.000015939328	0.000013707822	0.00000143454	0.00000000759	0
6	0.000112486115	0.000155750006	0.000026823612	0.000000288426	0
5	0.000526088909	0.001315222272	0.000394566681	0.000008768148	0
4	0.001249461158	0.007496766948	0.004373114053	0.000208243526	0
3	0	0.022343305413	0.03351495812	0.003723884236	0
2	0	0	0.141507600951	0.047169200317	0
1	0	0	0	0.377353602535	0
0	0	0	0	0	0.358485922409
Total	0.001905773455	0.031325747161	0.179818562032	0.428463994944	0.358485922409

The bottom row shows the probabilities for 0 to 4 distinct matches.

Acknowledgement: My thanks to Eliot J. for this help with this problem.