You are trapped in a small phone booth shaped room. In the middle of each side of the room there is a hole. In each hole there is a push button that can be in either an off or on setting. You can't see in the holes but you can reach your hands in them and push the buttons. You can't tell by feel whether they are in the on or off position. You may stick your hands in any two holes at the same time and push neither, either, or both of the buttons as you please. Nothing will happen until you remove both hands from the holes. You succeed if you get all the buttons into the same position, after which time you will immediately be released from the room. Unless you escape, after removing your hands the room will spin around, disorienting you so you can't tell which side is which. How can you escape? The fewest possible turns that I know if is seven.
(solution).
You are trapped in a small phone booth shaped room. In the middle of each side of the room there is a hole. In each hole there is a push button that can be in either an off or on setting. You can't see in the holes but you can reach your hands in them and push the buttons. You can't tell by feel whether they are in the on or off position. You may stick your hands in any two holes at the same time and push neither, either, or both of the buttons as you please. Nothing will happen until you remove both hands from the holes. You succeed if you get all the buttons into the same position, after which time you will immediately be released from the room. Unless you escape, after removing your hands the room will spin around, disorienting you so you can't tell which side is which. How can you escape? The fewest possible turns that I know if is seven.
(solution).

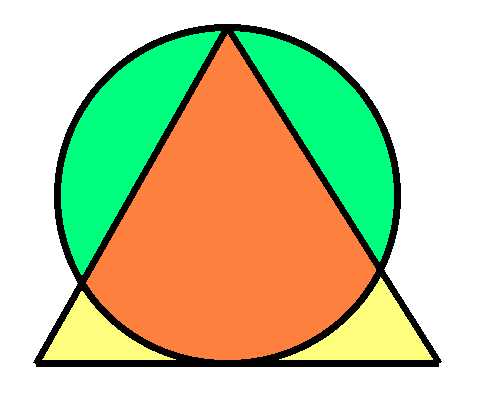
 There is a one acre field in the shape of a right triangle, with sides of length x and y. At the midpoint of each side there is a post. Tethered to the posts on each side is a sheep. Thethered to the post on the hypotenuse is a dog. Each animal has a rope just long enough to reach the two adjacent vertices of the triangle. How much area outside of the field do the sheep have to themselves?
(answer).
(solution).
There is a one acre field in the shape of a right triangle, with sides of length x and y. At the midpoint of each side there is a post. Tethered to the posts on each side is a sheep. Thethered to the post on the hypotenuse is a dog. Each animal has a rope just long enough to reach the two adjacent vertices of the triangle. How much area outside of the field do the sheep have to themselves?
(answer).
(solution).

 Each day a man meets his wife at the train station after work, and then she
drives him home. She always arrives exactly on time to pick him up. One
day he catches an earlier train and arrives at the station an hour early.
He immediately begins walking home along the same route the wife drives.
Eventually his wife sees him on her way to the station and drives him the
rest of the way home. When they arrive home the man notices that they
arrived 20 minutes earlier than usual. How much time did the man spend
walking?
(answer).
(solution).
Each day a man meets his wife at the train station after work, and then she
drives him home. She always arrives exactly on time to pick him up. One
day he catches an earlier train and arrives at the station an hour early.
He immediately begins walking home along the same route the wife drives.
Eventually his wife sees him on her way to the station and drives him the
rest of the way home. When they arrive home the man notices that they
arrived 20 minutes earlier than usual. How much time did the man spend
walking?
(answer).
(solution).
 Ten people land on a deserted island. There they find lots of coconuts and a monkey. During their first day they gather coconuts and put them all in a community pile. After working all day they decide to sleep and divide them into two equal piles the next morning. That night one castaway wakes up hungry and decides to take his share early. After dividing up the coconuts he finds he is one coconut short of ten equal piles. He also notices the monkey holding one more coconut. So he tries to take the monkey's coconut to have a total evenly divisible by 10. However when he tries to take it the monkey conks him on the head with it and kills him. Later another castaway wakes up hungry and decides to take his share early. On the way to the coconuts he finds the body of the first castaway, which pleases him because he will now be entitled to 1/9 of the total pile. After dividing them up into nine piles he is again one coconut short and tries to take the monkey's coconut. Again, the monkey conks the man on the head and kills him. One by one each of the remaining castaways goes through the same process, until the 10th person to wake up gets the entire pile for himself. What is the smallest number of possible coconuts in the pile, not counting the monkeys?
(answer).
(solution).
Ten people land on a deserted island. There they find lots of coconuts and a monkey. During their first day they gather coconuts and put them all in a community pile. After working all day they decide to sleep and divide them into two equal piles the next morning. That night one castaway wakes up hungry and decides to take his share early. After dividing up the coconuts he finds he is one coconut short of ten equal piles. He also notices the monkey holding one more coconut. So he tries to take the monkey's coconut to have a total evenly divisible by 10. However when he tries to take it the monkey conks him on the head with it and kills him. Later another castaway wakes up hungry and decides to take his share early. On the way to the coconuts he finds the body of the first castaway, which pleases him because he will now be entitled to 1/9 of the total pile. After dividing them up into nine piles he is again one coconut short and tries to take the monkey's coconut. Again, the monkey conks the man on the head and kills him. One by one each of the remaining castaways goes through the same process, until the 10th person to wake up gets the entire pile for himself. What is the smallest number of possible coconuts in the pile, not counting the monkeys?
(answer).
(solution).


 A 10 inch stick is thrown into a buzz saw and cut in two pieces at a random point. Each resulting piece is thrown into the buzz saw again, and each is again cut at a random point. What is the probability that all four remaining pieces are one inch long or greater?
(answer),
(solution).
A 10 inch stick is thrown into a buzz saw and cut in two pieces at a random point. Each resulting piece is thrown into the buzz saw again, and each is again cut at a random point. What is the probability that all four remaining pieces are one inch long or greater?
(answer),
(solution).
 On a game show there are three doors. Behind one door is a new car and behind the other two are goats. Every time the game is played the contestant first picks a door. Then the host will open one of the other two doors and always reveals a goat. Then the host gives the player the option to switch to the other unopened door. Should the player switch?
(answer),
(solution).
On a game show there are three doors. Behind one door is a new car and behind the other two are goats. Every time the game is played the contestant first picks a door. Then the host will open one of the other two doors and always reveals a goat. Then the host gives the player the option to switch to the other unopened door. Should the player switch?
(answer),
(solution).

 A column of soldiers one mile long is marching forward at a constant
rate. The soldier at the front of the column has to deliver a message to
the soldier at the rear. He breaks rank and begins marching toward the
rear at a constant rate while the column continues forward. The soldier
reaches the rear, delivers the message and immediately turns to march
forward at a constant rate. When he reaches the front of the column and
drops back in rank, the column has moved one mile. Question- How far did
the soldier delivering the message march?
(answer)
(solution).
A column of soldiers one mile long is marching forward at a constant
rate. The soldier at the front of the column has to deliver a message to
the soldier at the rear. He breaks rank and begins marching toward the
rear at a constant rate while the column continues forward. The soldier
reaches the rear, delivers the message and immediately turns to march
forward at a constant rate. When he reaches the front of the column and
drops back in rank, the column has moved one mile. Question- How far did
the soldier delivering the message march?
(answer)
(solution).
 How much is
How much is