Given n points drawn randomly on the
circumference of a circle, what is the probability they will all
be within any common semicircle?
(Answer),
(Solution).
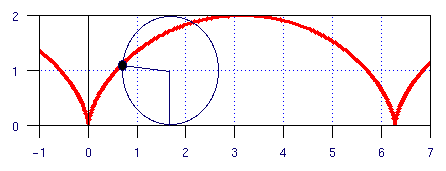
If you drew a dot on the edge of a wheel
and traced the path of the dot as the wheel rolled one complete
revolution along a line, then the path formed would be called a cycloid (shown
above), combining
both forward and circular motion. What is the length of the path
formed by one complete revolution? Assume the wheel has a radius of 1.
(Answer),
(Solution)
.
One morning is starts to snow at a
constant rate. Later, at 6:00am, a snow plow sets out to clear a
straight street. The plow can remove a fixed volume of snow per
unit time, in other words its speed it inversely proportional to
the depth of the snow. If the plow covered twice as much
distance in the first hour as the second hour, what time did it
start snowing? (Answer),
(Solution)
An ant and a blind spider are on opposite
corners of a cube. The ant is stationary and the spider moves at
random from one corner to another along the edges only. What is
the expected number of turns before the spider reaches the ant?
Optional: Also solve for a square, octahedron, icosahedron, and
dodecahedron.
(Answer),
(Solution)
While three wise men are asleep
under a tree a mischievous boy paints their foreheads red. Later
they all wake up at the same time and all three start laughing.
After several minutes suddenly one stops. Why did he stop?
(Answer),
(Solution)
There are two envelopes in front of you each with a non-zero number. You will receive an amount of money equal to the final envelope you choose. You are informed one has twice as much money as the other. You are then allowed to select either envelope. After you select one and before opening it you are given the option to change your mind and switch to the other one? You think to yourself that if your envelope has x dollars there is a
50% chance the other one has x/2 dollars and a 50% chance it has 2x dollars. The expected return, you compute, is .5[.5x +
2x]=1.25x which seems like a favorable gamble. Do you switch and
why? Assume you are neither risk averse nor risk prone, in other
words you will take any good gamble and avoid any bad one.
(Answer),
(Solution)
What is the volume of an tetrahedron
with edge length of 1?
(Answer),
(Solution)
What is the volume of an octahedron
with edge length of 1?
(Answer).
Simple numerical analysis required.
At McDonalds you can order Chicken McNuggets
in boxes of 6, 9, and 20. What is the largest number such that
you
can not order any combination of the above to achieve exactly the
number you want?
(Answer)
(Solution)
A town consists of only one street in the form of a circle. The town
authorities give out four licenses for a particular kind of business. The
inhabitants of the town live in equal density along the circle and will always
go to the closest business for what they need. Business A gets to choose a
location first, then business B, then C, and finally D. Each business
desires to carve out as much business for themselves as possible but each
knows the others all have the same motive. Assume that if a business is
indifferent between locating in two different sections of the circle it
will choose a section at random. Also assume that the business that
goes last will choose a location in the middle of the largest (or one of
the largest) sections.
Where should business B choose relative to the location of A?
(Answer)
(Solution)
Given a coin with probability p of landing on heads after a flip,
what is the probability
that the number of heads will ever equal the number of tails
assuming an infinite number
of flips?
(Answer)
(Solution)
Logical reasoning and basic math required.
Three men walk into a motel and ask for a room. The desk clerk
says a room is $30 so
each man pays $10 towards the cost. Later, the clerk realizes he
made a mistake, that
the room should have been $25. He calls the bell boy over and
asks him to refund the
other $5 to the three men. The bellboy, not wanting to mess with
a lot of change dividing
the $5 three ways, decides to lie about the price, refunding each
man $1 and keeping the
other $2 for himself. Ultimately each man paid $9 towards the
room and the bellboy got
$2, totaling $29. But the original charge was $30, where did
the extra $1 go?
(Answer)
(Solution)
Joe's happiness is proportional to the function w2*c (w squared * c), where
w stands for daily consumption of glasses of wine, and c stands of
daily consumption of number of cigars. Wine costs $3 a glass and
cigars cost $2 each. His daily budget for both is $100. How should
he divide his money between wine and cigars to maximize his
happiness? Assume he does not have to buy integer numbers of either
cigars or wine.
(Answer),
(Solution).
A bartender has a three pint glass and a five pint glass. A customer walks in and orders four pints of beer. Without a measuring cup but with an unlimited supply of beer how does he get four pints in either glass?
(Answer & Solution)
Assume you have a checker board with 7 rows and infinite columns.
You can
place checkers on only the first 2 rows initially. Then you may
jump other
checkers up, down, right, and left but not diagonally.
The
goal is to get as high a row as possible. For example you can
get to the
second level with four checkers like this:
Initial
Level setup Turn 1 Turn 2 Turn 3
----- ------- ------ ------ ------
2 a
1 d d
0 abc ab a
-1 d
It turns out you need 2 checkers to get to level 1, 4 to get to
level 2, 8 to
get to level 3, 20 to get to level 4, but it is impossible to get
to level 5.
The question is to prove that it is impossible to get to level 5.
(Answer & Solution)
Integral calculus required.
A dart is thrown at a circular dart board of radius one. The dart can land at
any place on the dartboard with equal probability. What is the mean distance
between where the dart hits and the center of the board?
(Answer),
(Solution).
The gas tank of a truck is cylindrical in shape with a radius of r inches and a
lengh of l inches, and tank lays on its side. With a measuring stick you note how many
inches of gas are in the tank. Given this depth of gas, how many cubic inches of gas are in the tank?
You may assume the tank is less than half full.
(Answer),
(Solution)
You have an urn with four balls of different colors. Randomly you
draw two at a time, then painting the first ball to match the second.
What is the expected number of drawings before all balls are the
same color?
(Answer),
(Solution).
You are a cook in a remote area with no clocks or other way of
keeping time
other than a 4 minute hourglass and a 7 minute hourglass.
You do have
a stove however with water in a pot already boiling. Somebody
asks you for a
9 minute egg, and you know this
person is a perfectionist and will be able to tell if you
undercook or overcook
the eggs by even a few seconds. What is the least amount of time
it will
take to prepare the egg?
(Answer),
(Solution).